|
The Milky Way Galaxy (see
the wikipedia
definition)
TOC:
Rotation curve of the MW galaxy (go to top)
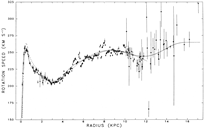
- (Clemens, 1985ApJ...295..422C)
Facts: They use the Massachusetts-Stony Brook Galactic Plane CO survey, together with literature data of HI in the nuclear region, CO observations of HII regions, and globular clusters in the outer Galaxy to constrain the rotation curve of the Galaxy.
Results: The rotation curve are shown in figure and piecewise polynomial fittings are given:
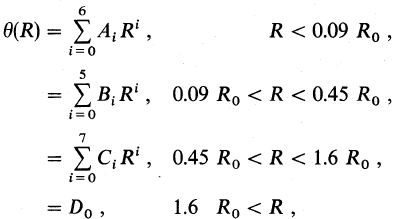 with coefficents: with coefficents: 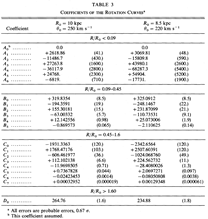 . .
(figs: left -- the rotation curve for R0=10kpc, V0=220km/s; right -- the rotation curve for R0=8.5kpc, V0=220km/s. Note: full line is the polynomial fit, dashed line is Burton & Gordon fit.)
- (Fich et al., 1989ApJ...342..272F)
Facts: They use the HI tangent points inside the solar circle and CO observations of HII regions out side of the solar circle to constrain the rotation curve of the Galaxy.
Results: Their find that a flat rotation curve of V = 220 km/s can be used for the outer Galaxy in the range of 3-17 kpc.
- (Reid et al., 2009ApJ...700..137R)
Facts: They use VLBI measurements of masers in 18 high-mass star-forming regions to constrain the Galaxy model.
Results: Their findings:
(1) star-forming regions are orbiting the Galaxy about 15 km/s slower than expected for circular orbits;
(2) confirm that the rotation curve is nearly flat or slightly rising with increasing Galactocentri radius;
(3) the angular velocity of the Sun (30.3 km/s/kpc) is significantly larger than the IAU value of 25.9 km/s/kpc;
(4) the kinematic distance is usually too large, sometimes by a factor of 2. A new approch to estimate the kinematic distance and Fortran code is offered;
(5) the parameters are very similar as another dominant Local Group galaxy, M31 (Andromeda), indicating that their dark matter halos are similarly massive.
(6) their new parameters:
GC-Sun distance R0 = 8.4 ± 0.6 kpc;
circular rotation speed of the Sun V0 = 254 ± 16 km s−1,
angular velocity of the Sun V0/R0 = 30.3 ± 0.9 km s−1 kpc−1,
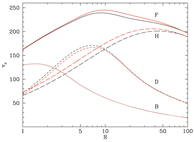
- (McMillan, 2011MNRAS.414.2446M)
Facts: He use a simple parameterized mass model to fit the observational constraints of the Milky Way galaxy.
Results: His findings:
scalelength of the thin disc: Rd,thin = 3.00±0.22 kpc,
scalelength of the thick disc: Rd,thick = 3.29±0.56 kpc,
solar radius R0 = 8.29 ± 0.16 kpc,
circular speed of the Sun V0 = 239 ± 5 km/s,
total stellar mass 6.43 ± 0.63 ×
10^10 Msun,
virial mass 1.26 ± 0.24 × 10^12 Msun, and a
local dark matter density 0.40 ±
0.04 GeV cm−3.
In the end, he concluded that the mass model of the MW galaxy is still very uncertain.
(fig: the model rotation curve (black full line) and the the contribution from different components: B = bulge, D = disc, H = dark matter halo. The red lines are for the convenient model (with convenient parameter values).)
Structure of the MW galaxy (go to top)
- (Lockman, 1989ApJS...71..469L) provided radio H recombination line data of nearly 500 HII regions, which could be used to study the spiral arm of the Galaxy.
- (Combes, 1991ARA&A..29..195C) reviewed the distribution of CO in the Milky Way galaxy. (downloaded, to read.)
- (Vallee, 1995ApJ...454..119V)
Facts: All literature upon Milky Way Galaxy structure between 1980-1994 are collected together to yield an weighted average of spiral models for the MW galaxy. The methods used in these literature are: (1) magnetic field direction determined from pulsar RM; (2) magnetic field direction determined from RM of QSOs and galaxies; (3) dust map; (4) CO and H2 maps; (5) HI map; (6) thermal electrons gas (pulsar DM); (7) HII regions; (8) location of stars and star associations. Although studies of other galaxies show that disk galaxies can be of different morphological classes ranging from flucculent to grand-design spirals, to derive a mean spiral model for the Galaxy, they still assume that the Milky Way galaxy is a spiral arm galaxy and the arms are all ideal logarithmic spiral regions within which the emission intensity on the whole disk can be described by
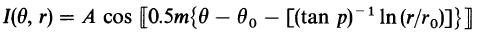
where A, θ0 and r0 are constants, p is the pitch angle, m is the number of arms that are rotation symmetrically arranged in the disk, θ and r are the position variables. For an inward arm (that spiraling to a smaller r when θ increases), we have p>0 deg, θ>0 deg. The central track (backbone) of the arm structures are at
ln(r/r0) = tan(p) (θ-θ0)
The arm separation between neighbouring arms at a direction along which the radius is r1 for the inner arm and r2 for the outer arm, the arm separation can be obtained from the arm radius ratio:
2π tan(p)
= m ln(r2/r1)
Results: They determined: Rsun = 8 kpc, m = 4, p = 12 deg, r0 = 2.5 kpc, θ0 = 0, 90, 180, 270 deg.
(fig. the logarithmic 4-spiral pattern of the fitted Milky Way model.)
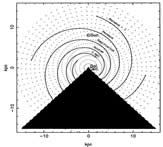
- (Vallee, 2002ApJ...566..261V)
Facts: All literature upon Milky Way Galaxy structure between 1995-2001 are collected together to yield an weighted average of spiral models for the MW galaxy. To derive a mean spiral model for the Galaxy, they assume the arms are all ideal logarithmic spiral as in his previous paper (paper I).
Results: They determined: Rsun = 7.2 kpc, m = 4, p = 12 deg, r0 = 2.3 kpc, θ0 = 0 (Norma), 90 (Perseus), 180 (Sagittarius), 270 deg (Scutum), with θ0 = 0 started from the stellar bar at a angle of 30 deg w.r.t. Sun-GC line. The interarm separation is 2.5 kpc, and the Sun to Sagittarius arm distance is 0.9 kpc.
(fig. the logarithmic 4-spiral pattern of the fitted Milky Way model.)

- (Holpak et al., 2003ApJ...582..756K)
Facts: They used the VLA observation of 21cm HI absorption lines towards 49 HII regions to differentiate the near and far kinematic distances.
Results: The kinematic distances are determined for the 49 H II regions. The spatial distribution of them show signiture of sprial arm segments. The H II regions also coincident with CO cloud distribution. There are 3 times more H II regions are at far Dkin than at near Dkin, due to geometrical effect (say, for a given solid angle, the far side has much larger spatial volumn).
- (Bissantz et al., 2003MNRAS.340..949B)
Facts: They did SPH simulations to study the gas dynamics in the gravitational potential.
Results: They confirm that four-arm model, with different pattern speeds between the bar and arms, reproduce the observations better. The bar pattern speed is Ωp=60±5Gyr^-1, corresponding to corotation at 3.4±0.3 kpc; the spiral pattern speed is Ωsp=20Gyr^-1. The bar angle w.r.t. the GC-Sun line is φbar=20-25deg.
- (Vallee, 2005AJ....130..569V)
Facts: All literature upon Milky Way Galaxy structure between mid-2001--2005 are collected together to yield an weighted average of spiral models for the MW galaxy. To derive a mean spiral model for the Galaxy, they assume the arms are all ideal logarithmic spiral as in his paper I.
Results: They determined: Rsun = 7.9 kpc, m = 4, p = 12 deg, r0 = 2.52 kpc, θ0 = 0 (Norma), 90 (Perseus), 180 (Sagittarius), 270 deg (Scutum), with θ0 = 0 started from the stellar bar at a angle of 30 deg w.r.t. Sun-GC line. The interarm separation is 2.74 kpc, and the Sun to Sagittarius arm distance is 1.0 kpc.
(fig. the logarithmic 4-spiral pattern of the fitted Milky Way model.)

- (Benjamin et al., 2005ApJ...630L.149B)
Facts: They report in the letter the first results of point sources identified from the Spitzer/GLIMPSE survey.
Results: About 30 million point sources are identified in the inner Galaxy (10deg < l < 65 deg; |b| < 1 deg). Exponential disk model parameters are determined by fitting the data: radial scale length H* = 3.9 +-0.6 kpc, a liner GC bar with half-length Rbar = 4.4 +- 0.5 kpc, tilted by φ = 44 +- 10 deg w.r.t. GC-Sun line.
- (Vallee, 2008AJ....135.1301V)
Facts: All literature upon Milky Way Galaxy structure between mid-2005 to mid-2007 are collected together to yield an weighted average of spiral models for the MW galaxy.
Results: (1) Rsun = 7.6 kpc, m = 4, p = 12.8 deg, r0 = 2.1+-0.1 kpc, θ0 = -20+-5deg (Norma), 90 (Perseus), 180 (Sagittarius), 270 deg (Scutum), with θ0 = 0 started from the stellar bar of 3.1 kpc half-length and at a angle of 32 deg w.r.t. Sun-GC line. Interarm distance at the Sun's direction = 2.76 kpc.
(2)
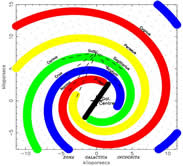
He also propose that the so-called 4-pkc molecular ring actually does not exist, instead, it is the overlap of the starting ends of the four spiral arms along the lines of sight.
(3) He adopted a flat rotation speed of 220 km/s for r_gal > 2 kpc (scaled for Rsun = 7.6 kpc in this paper) to compute the l-vr relations for the four spiral arms. Here vr is the velocity of material at r w.r.t. the Sun:
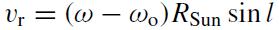
where ω and ω0 are the angular velocity of the material at GC radius r and the Sun, respectively. According to Kepler's second law, the mass within a radius r can be calculated as
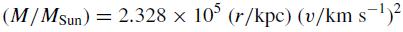
where v is the circular motion velocity at radius r. Given the fact that the circular motion velocity is nearly constant (220 km/s for Rsun = 7.6 kpc) at most radii, the mass is a linear function of r. (It includes the dark matter mass.) Thus the mass within the solar circle is ~1x10^10 Msun.
(fig. left -- the logarithmic 4-arm spiral pattern of the fitted Milky Way model (red=Norma-Cygnus; blue = Scutum-Crux; green = Sagittarius-Carina; yellow = Perseus); right -- the l-vr relation of the 4-arm spiral model.)
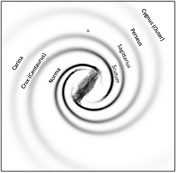
- (Churchwell et al., 2009PASP..121..213C)
Facts: They reviewed the main results form the Sptizer/GLIMPSE survey, including areas surveyed, sensitivity limits and products. (Here I only collect the information about the Milky Way Galaxy structure.)
Results on Galactic structures: (1) GLIMPSE provides for the strongest evidence and parameters for the central stellar bar: radius = 4.4+-0.5 kpc, orientation = 44 +- 10 deg w.r.t. to Sun-GC line;
(2) the stellar disk is an exponential disk with radial scale-length of 24.2+-0.3 deg or 3.9+-0.6 kpc (determined using red clump giants whose MK = -1.62+-0.03 mag and (J-Ks)o = 0.7 mag). The stellar disk is very flat (with fluctuation of no more than 0.05 deg).
(3) the spiral arm structure reconstructred on the basis of all observational clues obtained in the last 50 years (see the figures below).
The basic features are:
(3.1)
the Sun-GC distance is taken as 8 kpc;
(3.2)
the Galactic bar (= COBE/DIRBE bar = the triaxial bulge = the bulgery-bar): aspect ratios of 10:4:3, half length of 3.1-3.5 kpc, orientation angle = 20 deg w.r.t. GC-Sun line;
(3.3)
the long bar;
(3.4)
Near and far 3-kpc arms: discovered from HI and CO observations;
(3.5)
Outer spiral arms: with tweaks from VLBI observations, refined tangencies from CO survey, and adjustment of the amplitude to fit the association with the two stellar arms.
The author remarks that the spiral arms are the most uncertain elements in this pattern.
(figs: left -- the MK galaxy structure; right -- the annotated version.)
 
- (Hou et al., 2009A&A...499..473H)
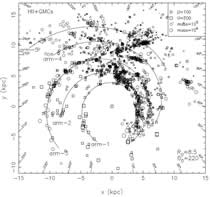
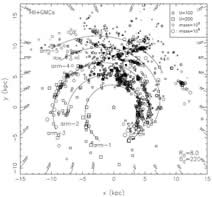
Facts: They collected observational data of H II regions and giant molecular clouds (GMCs) to outline the spiral structure of the Galaxy.
Results: (1) none of the 2, 3 or 4-arm logarithmic spiral model can fit all observational tangents (failed to the tangents of Scutum, Sagitarrius and Norma arms).
(2) They proposed polynomial spiral model that fit all the data well: ln(r) as a cubic function of θ.
(figs: left -- the polynomial spiral model overplotted upon H II and GMCs with R0=8.5 kpc, theta0=220 km/s; middel -- with R0=8.0 kpc, theta0=220 km/s; right -- with R0=8.4 kpc, theta0=254 km/s)
  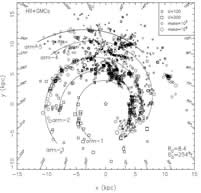
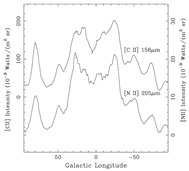
- (Steiman-Cameron, et al., 2010ApJ...722.1460S)
Facts: They compared verious Galactic spiral arm models with [CII] 158 um and [NII] 205 um lines from FIRAS instrument on board COBE, data from the Balloon-borne Infrared Carbon Explorer and ISO to validate the spiral arm structure of the Galaxy. N II only comes from H II regions (due to high ionization potential of 14.5 eV), while C II can come from both H II regions and diffuse ionized medium.
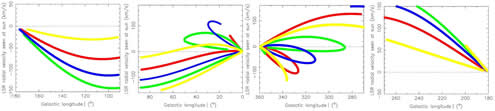
Results:
(1) Longitude distribution of integrated intensity of the [CII] and [NII] lines show smooth trends upon which local maxima are clearly seen around l = +80, (+50,) +30, -22, -51, and -73 deg, in agreement to discoveries through other spiral tracers such as radio continuum, HI emission, synchrotron emission, H109α, warm CO, integrated 12CO, 1.8 MeV γ-ray from the decay of 26Al, and dust thermal emission. (Note: the l = +50 peak is interpolated from off-plane data.)
(2) The very strong peak at l = +80 deg (toward Cygnus X) is the local arm -- Orion spur, which is not a globle feature and are not considered in their modeling.
(3)
Only four-arm model is fully and nicely supported by current observation data and historical observations (three-arm model can also reproduce the observation data but was never proposed by previous studies);
(4) the preferred model has four well-defined logarithmic spiral arms in the gaseous ISM;
(5) previous two-arm models are all deduced from observations of old evolved stars (K and M giants) , they are coincidant with the two strongest arm found in this work;
(6) the two-stellar-arm and four-gaseous-arm dichotomy could be explained by two scenarios: 1) unusually large extinction toward W 51, the Sagittarius tangency direction; 2) the stellar arms could be really different from the gaseous arms.
(7) from their derived spiral arm model, they constrain the half-length of the bar < 3 kpc * (Rsun/8.5kpc).
The shape functiion of the logarithmic spiral form adopted in their is
r = a eαφ or φ = ln(r/a)/α,
where r is the radius, φ is the angular variable and a and α are parameters.
The assumed functional form of the CII and NII emissivity in the arm models is
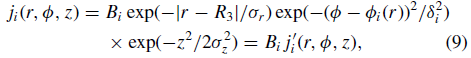
where Bi is the scaling factor for the i'th arm and the other parameters are R3 -- the characteristic radius where the spiral arm has thestrongest CII and NII emission, σr, σz -- the scale length along the radial and z directions (the same for all four arms), δi -- the scale length along the azimuth direction (can be different for individual arms). They considered a disk component superimposed upon the spiral component, but did not find any clue to support its existence in their data.
The best fit parameters are
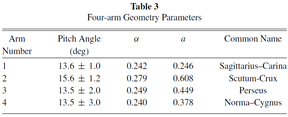 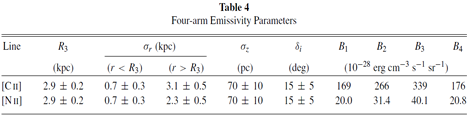
(figs: left --integrated emission strength distribution of CII and NII; right -- derived gaseous four-spiral pattern.)
Dark matter in the MW galaxy (go to top)
- (Navarro et al., 1997ApJ...490..493N)
Facts: They performed large amound ot N-body simulation upon individual dark matter halos.
Results: (1) They found that equilibrium dark halos formed through dissipationless hierarchical clustering have universal density profiles that are independt of their mass, initial perturbation power spectrum, or cosmological parameters Ω0 and Λ.
(2) Density profile of an isolated equilibrium halo can be specified quite accurately by giving two parameters: the halo mass and the halo characteristic density.
(3) The characteristic halo density is proportional to the density of the universe at the collapse time of the objects that merge to form the halo core.
(4) They give an analytical procedures to compute the dark matter halo density profile of a given mass (offering Fortran code for this).
- (Olling & Merrifild, 2000MNRAS.311..361O)
Facts: They used the rotation curve, kinematics of nearby stars, and the radial distribution of HI thickness to constrain the shape of the Milky Way dark matter halo.
Results: They found a flattening of shortest-to-longest axies ratio of q=0.8, but only for a pair of non-standard parameters R0<7.6 kpc and V0<190 km/s for the Sun. Thus, this value needs further confirmation.
- (Binney & Evans, 2001MNRAS.327L..27B)
Facts: They estimated the minimum total baryonic matter mass in our barred spiral Galaxy.
Results: The baryonic mass within the solar circle is no less than 3.9x10^10 Msun, which controdict with any cuspy dark matter halo model.
- (Klypin et al., 2002ApJ...573..597K)
Facts: They apply standard disk formation theory with adiabatic contraction within cuspy halo models predicted
by the standard cold dark matter (ΛCDM) cosmology. The simulation is compared to observational data of the Milky Way and M31 galaxies.
Results: The find good fits only in a narrow parameter space:
Milky Way: virial mass = 10^12 Msun, average spin parameter λ = 0.03-0.05, concentration Cvir = 10-17.
M31:
virial mass = 1.6x10^12 Msun, average spin parameter λ = 0.03-0.05, concentration Cvir = 10-17.
(2) assuming the baryonic disk can loose part of angular momentum to the dark matter halo through dynamical friction, a fast rotating bar can persist at the center, and the mass of baryonic matter nera the GC could be enough to explain the optical depth observed by microlensing. The angular momentum transfer to dark matter also helps propel the dark matter out of the GC.
(3) They used the formulae of Navarro et al. (1997, see above) for a cosmological model of Hubble constant H0 = 70 km/s/Mpc and the contribution of matter (dark + baryonic) to the critical density Ω0 = 0.3:
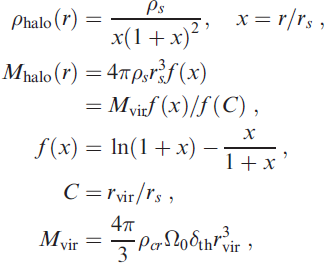
where C and Mvir are the halo concentration and virial mass, and rvir is the virial radius. The other parameters are the critical density of the universe ρcr and the overdensity of a collapsed object in the 'top-hat' collapse
model δth (=340 in this model). The two independent parameters C and Mvir define all properties of the halo. However, in a real ΛCDM model, the C and Mvir are actually correlated according to
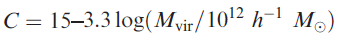 , ,
with a 40% of statistic fluctuation. For a Mvir = 10^12 Msun halo, this gives C = 11~21. But, for a Sb type galaxy like the Milky Way, C should be in a narrower range. They tentatively adopted C = 10-17. A more general density profiles of dark matter halos should be a double power law of the form
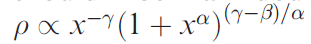
where x is the rescaled radius, γ, β, and α prescribe the steepness of the inner cusp, the outer slope, and the sharpness of the transition, respectively
(Zhao 1996a). Consequently, usually the dark matter halo formation models have an inner cuspy density profile ρhalo ~ r-γ, with 1 < γ < 1.5. However, they still adopt the set of formulae above which have this effect neglected.
- (McMillan, 2011MNRAS.414.2446M)
Facts: He use a simple parameterized mass model to fit the observational constraints of the Milky Way galaxy.
Results: His findings:
scalelength of the thin disc: Rd,thin = 3.00±0.22 kpc,
scalelength of the thick disc: Rd,thick = 3.29±0.56 kpc,
solar radius R0 = 8.29 ± 0.16 kpc,
circular speed of the Sun V0 = 239 ± 5 km/s,
total stellar mass 6.43 ± 0.63 ×
10^10 Msun,
virial mass 1.26 ± 0.24 × 10^12 Msun, and a
local dark matter density 0.40 ±
0.04 GeV cm−3.
In the end, he concluded that the mass model of the MW galaxy is still very uncertain.
(fig: the model rotation curve (black full line) and the the contribution from different components: B = bulge, D = disc, H = dark matter halo. The red lines are for the convenient model (with convenient parameter values).)

-
|
![]()