Formulae of molecules and atoms (radio spectra)

Meaning of quantum numbers and related symbols

(Most contents from NIST diatomic spectral database documents)

I or I_i – Angular momentum quantum number of nuclear spin for one (or ith) nucleus

S – Resultant angular momentum quantum number of electron spins

Σ – Projection of S on the molecular axis (for Hund’s case a only)

Λ – Absolute value of the projection of the resultant orbital electronic angular momentum on the molecular axis (for Hund’s case a and b only)

Ω – Absolute value of the projection of the total electronic angular momentum on the molecular axis (= Σ+Λ)

N – Rotational angular momentum quantum number, excluding electronic and nuclear spins

J – Resultant total angular momentum quantum number, excluding nuclear spins

m_J – Projection of J along any given axis

F_i – Resultant angular momentum quantum number including nuclear spin for i nuclei

I_tot – Resultant angular momentum quantum number of two or more nuclear spins that couple together before being coupled into total rotational angular momentum F.

F – Resultant total angular momentum quantum number

m_F – Projection of F along any given axis

X – Quantum number employed when F_i’s are not good quantum numbers. This value simply numbers the levels from lowest to highest energy for the same F quantum number

v – Vibrational quantum number

ν_i – vibrational quantum numbers for the ith vibrational mode for molecules with more than 2 nucei. Vibrational modes are usually sorted with increasing energy (with decreasing degree of symmetry) and designated as ν₁, ν₂, ν₃,… sequentially.

l – Quantum number for the projection of degenerate 2-dimensional bending vibration angular momentum on molecular axis (for linear molecules only)

Σ, Π, Δ -- Electronic state designation for which Λ = 0, 1, 2, respectively. The symbols X, A, B, E, F, … precede the state designation where X refers to the ground state, A refers to the first excited electronic level, ...

General Formulas

Radiative transfer

The general radiative transfer equation for a ray is

,

where I_ν is the radiation intensity in ergs^-1cm^-2Hz^-1sr^-1, s is the radiation transfer route length, κ_ν is the absorption coefficient (opacity) in cm^-1, ε_ν is the emission coefficient (emissivity) in ergs^-1cm^-3Hz^-1sr^-1. It is convenient to define an optical depth τ_ν as

.

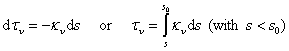Note that both τ_ν and s are positive quantities, while the minus sign in the first equation means the two quantities increase in opposite directions, with τ_ν =0 at s₀. The radiation is going along increasing direction of s. Then, the radiation transfer equation becomes

,

with the source function

.

In thermodynamic equilibrium (TE), I_ν= S_ν= B_ν(T_k), with T_k being the kinematical temperature of gas (e.g., in the interior of a star). Here, the Plank function is

For molecular gas not in TE but in local thermodynamic equilibrium (LTE), although the radiation is not in equilibrium with the gas, we usually still can define an single excitation temperature T_ex for all energy levels of a molecule (according to Boltzmann distribution, see below), so that S_ν= B_ν(T_ex) can be fulfilled for all transitions. Even when the molecular gas is not in LTE, this definition of T_ex still can be applied, but T_ex may be different for different transitions of the same molecule.

The formal solution of the radiative transfer equation is

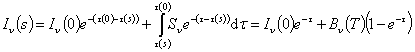
In the second equation, we have replaced the optical depth difference τ(0)- τ(s) by a new optical depth τ that is defined to be zero at s=0 and increases in the same direction as s. If we subtract the back ground intensity I_ν(0)= B_ν(T_bg) from the measured intensity I_ν(s), we get

,

or in terms of brightness temperature

.

Here, T_R is the brightness temperature directly measured by radio telescope using the beam switch method (so that the back ground brightness has been subtracted). J(T) is Relaigh-Jeans temperature:

Einstain coefficients A_ul, B_ul and B_lu

The three Einstein coefficients that describe the interaction between molecule and radiation are the spontaneous transition probability A_ul in s^-1, the induced emission or absorption probability B_ul and B_ul in s^-1erg^-1cm²sr. For gaseous molecule with radiative transitions between an upper level “u” and a lower level “l”, the three coefficients are defined by

Here, f_lu is oscillator strength, e is electron charge, m_e is electron mass, c is the speed of light, ν is the transition frequency from upper, g_u, g_l are statistic weights. Therefore, for gas number density n_u and n_l in the two levels, the spontaneous photon emission rate is n_uA_ul (s^-1) while the induced photon emission or absorption rates in a radiation field with mean radiation intensity of J(ν_ul) (erg/s/Hz/cm²/sr) are n_uB_ulJ(ν_ul) and n_lB_luJ(ν_ul) (s^-1), respectively. (NOTE1: The definition of B_ul and B_lu may be slightly different by using radiation energy density U(ν_ul) instead of the mean intensity J(ν_ul) according to the relationship .) (NOTE2: If the levels are degenerate, the above emission rates are only for transition from one initial sublevel to all final sublevels. Therefore, to calculate the total emission rates, one must multiply them by the statistic weight of the initial level.)

The Einstein coefficient A_ul is related to the electric or magnetic dipole moment μ_ul of the transition as

.

For rotational transitions, the dipole moment is usually expressed as

,

in which μ_x is the permanent dipole moment along axis x (the symmetry axis of a molecule along which the permanent dipole moment is non-zero), ^xS_ul is the so called line strength or transition strength for the transition from level “u” to “l”. The line strength is only determined by the direction part of the molecular wave function and so is only related to the symmetry property of the molecule. Especially, the line strength has no relation to molecular weight, size, composition etc. The formulas of the line strength for molecules with different symmetry types are given in detail in latter sections.

Absorption coefficients in terms of Einstein coefficients

Absorption coefficient per unit volumn of molecular gas is

.

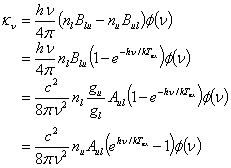From here on, the subscript “ul” of frequency has been omitted for clarity. Substituting A_ul into this formula, one gets

Boltzmann distribution

In local thermal equilibrium (LTE), the molecular energy level population distribution n_j obeys the Boltzmann distribution law

,

in which N is the total number density, T_k is the kinematical temperature, E_j is the energy of the level j, and Q is the partition function which is defined as

.

One must be careful about the calculation of Q when fine structure or hyperfine structure lines are considered. For those molecules with non-zero electron and/or nuclear spins, the (hyper-) fine-structure splitting increases the total number of levels and makes the Q value much larger. Therefore, with the same number density N, the population n_j of each (hyper-) fine level becomes smaller, and the individual (hyper-) fine line intensity also becomes weaker. This consideration is also valid for those asymmetric top molecules that have many energy levels due to the lack of symmetry.

Relative intensity of optically thin rotational lines

In the case of optically thin case, we can omit the opacity effect and use the spontaneous photon emission rate to roughly estimate the relative intensity of different rotational lines. For a homogeneous and optically thin molecular cloud, we can omit the opacity effect so that the integrated emission line intensity just equals to

Here, the formulas of the Einstein A coefficient and the boltzmann distribution law have been applied. With the formulas for pure rotational transitions given in latter sections: and, one has

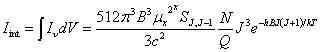
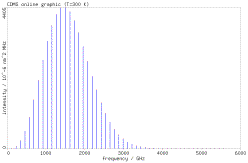
The strongest line occurs at . Take the example of CO in the ground vibration state, B=57635.968 MHz from CDMS database. Therefore, the strongest optically thin is at. For a temperature of T = 9.375 K, the strongest line is at around J=2. For T = 300 K, the strongest line is around J=12.5. These results qualitatively agree with the line intensity plots from CDMS database (see in the figures below).

028503 CO, v=0

028503 CO, v=0

Rotation diagram analysis

Although further extension of above discussions of relative intensity of optically thin lines just results in the formula for rotation diagram analysis (See for example the derivation by Cummins et al., 1986, ApJS, 60, 819), here I would like to restart from the formal solution of radiative transfer equation to derive it. From the formal solution of RT equation, the observed radio line intensity after the removal of back ground emission is

.

Here, Rayleigh-Jeans approximation has been applied to T_ex and T_bg. In the optically thin case,

From above discussions of absorption coefficient, one has the optical thickness of a homogeneous cloud as

.

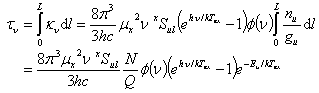Here, L is the size of the cloud, N is the total column number density of the molecules and Q is the partition function. Substituting it into previous formula and integrate over frequency, one gets the integrated line temperature

By using the relation and applying Rayleigh-Jeans approximation, we have the integrated line intensity

.

Then we obtain the standard formula for rotation analysis:

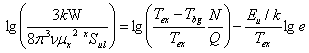
(See the similar derivation by Kawaguchi et al., 1995, PASJ, 47, 853) Note that this formula is applicable only for energy levels (in unit of K) far lower than kinematical temperature of the gas. Otherwise, non-LTE effects may emerge.

Energy level balance equations (Rate equations)

In above discussions, TE or LTE has been assumed. However, the actual molecular gas may not fulfill that condition. For example, when external radiation field plays an important role in the excitation of energy levels, LTE is usually not met. In this case, one needs to compute the level populations by the level balance equations:

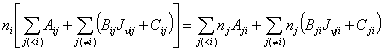
Here, A_ij and B_ij are Einstein constants, C_ij is collision rate in unit of s^-1, J_νij is the mean radiation intensity in unit of Wm^-2Hz^-1Sr^-1 that must be determined by solving radiative transfer equation. This set of equation must be closed by the equation of particle conservation

Here N is total number density of the species. Once the mean radiation intensity is known, these linear equations of level population can be easily solved by standard method.

Format of molecular energy level specification

Similar as atomic energy level formulas, molecular formula also take the form

Here the terms before the parenthesis is electronic state specification. X means it is in the ground electronic state (n=0). X may be replaced by A, B, C, … for excited electronic states with n=1, 2, 3, … However, molecules in electronically excited states are rare, because the huge excitation energy usually will get the molecule dissociated. In the second electronic term, Λ represents projection of resultant electronic orbital angular momentum along the major symmetry axis of the molecule. Upper case Greek letters Σ, Π, Δ, … are used for |Λ| = 0, 1, 2, … respectively. However, for strongly asymmetric molecules for which there is no obvious symmetry axis, the Greek letters may be replace by upper case alphabets A, B, E, F, … to indicate the different symmetry properties. S is the total electron spin quantum, hence 2S+1 is also called multiplicity of each electronic level. Ω represents the resultant projection of total electronic angular momentum along the major symmetry axis of the molecule (mainly composed of projection of electronic spin Σ and that orbital angular momentum Λ, but in the case of bending linear molecules, it also include the projection of the 3D bending angular momentum l).

The quantum numbers (Qn) in the parenthesis are related to vibration and rotation of the molecule. Those Qns not related to spin are usually called primary Qns, while those involving spins are called secondary Qns. The Qn v is for vibrational states of diatomic molecules, while ν_i^l is used for linear chains where i = 1, 2, 3, … for different vibrational frequency modes ν₁, ν₂, ν₃, …. The superscript l is for the projection of the 3D vibrational angular momentum along the symmetry axis. N is the Qn for rotational angular momentum, J is the Qn for resultant total angular momentum (including electronic components), Ω is the Qn for resultant total angular momentum in the Hund’s case (a) coupling, Λ is the Qn for projection of resultant total angular momentum along symmetry axis. The rest are secondary Qns: F₁, F₂, …F_i, … are for resultant angular momentum when the ith non-zero nuclear spin is taken into accound; I_tot is the resultant of nuclear spins of two identical nuclei that usually couple first before being coupled to the total angular momentum; F is for the ultimate total angular momentum (the only quantity that strictly conserves).
Atoms

(Most contents from chapter 5 of Townes C.H. and Schawlow A.L., Microwave Spectroscopy, New York: McGraw-Hill, 1955)

Quantum numbers

Usually, only hyperfine structure transitions of atoms appear in millimeter wavelength. Quantum numbers for an atomic level with nuclear spin are L, J, m_J, I, F, m_F.

Energy level

There are mainly two kinds of hyperfine structure splitting due to electric quadrupole momentum and magnetic dipole momentum respectively. The formula of quadrupole hyperfine structure level is

With

Here, eq_JQ is the quadrupole coupling constant.

The formula of magnetic dipole hyperfine structure level is

Here, a is the so-called interval factor, a constant for a given electronic state and nucleus.

With external magnetic field, ……(Zeeman effects)

Statistic weight

For the pure hyperfine structure level: S_F = 2F+1

Selection rules

Only pure hyperfine transitions fall in microwave. The selection rule for these pure hyperfine transitions is

Magnetic dipole moment for the transitions

The pure hyperfine transitions in microwave are usually only strong in the ground electronic state ²S_1/2 of atoms, because most atoms in space are populated in this ground level and the hyperfine structure splitting is the largest in this state. For pure hyperfine transitions in the ²S_1/2 state with external magnetic filed, the magnetic dipole moment for transition is:

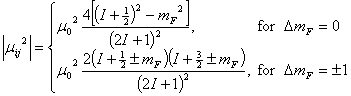
Here, m_F is the projection of total angular momentum F along the direction of external magnetic filed B, μ₀ = he/4πmc is the Bohr magneton (the statistic weight for each non-degenerate magnetic level is 1). Note that the transitions with are always polarized with their magnetic vector parallel to magnetic filed B, while transitions with are always polarized with their magnetic vector perpendicular to magnetic filed B.) The line strength in this case is

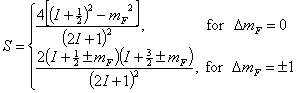
For pure hyperfine transitions without external magnetic field, the magnetic dipole moment averaged over all transitions with the same Δm_F and summed over 3 directions for absorption transition is

The line strength in this case is

Inversely, the magnetic dipole moment for emission transition should be

,

Here, g_F = 2F+1 = 2(I+1) is the statistic weight of each level.

Miscellaneous

l Angular momentum of an electron:

l Magnetic moment of an electron: (μ₀ is the Bohr magneton, is the fine structure constant.)

l Angular momentum of a nucleus:

l The most famous example of pure hyperfine structure transition is the 21cm H emission line (1.420405 GHz) from the interstellar space of the Galaxy.

Diatomic molecules

(Most contents from chapter 1 of Townes C.H. and Schawlow A.L., Microwave Spectroscopy, New York: McGraw-Hill, 1955)

Quantum numbers (my opinion)

For simple diatomic molecules: J(=N), v (e.g., X¹Σ state molecules)

with only fine structure splitting: N, v, J (e.g., X³Σ state molecules)

with only hyperfine structure splitting: J(=N), v, F₁, F

with both fine and hyperfine structure splitting: N, v, J, F₁, F

for Hund’s case a coupling (L>0,S>0): Ω, Λ, J (e.g., X²Π state molecules)

for Hund’s case a with hyperfine structure: Ω, Λ, J, F₁, F (e.g., OH)

Here, N, v, Ω, Λ are called principal quantum numbers, J, F₁, F are called spin involved quantum numbers. For molecules with identical nuclei, the sign of Λ should reflect parity. F₁ is needed only when both nuclei have non-zero spin. In the case where J=N, the convention is to use J and omit N.

Energy level

For a rigid rotor with neither electronic nor nuclear spin, level energy

,

where h is Plank’s constant, I is the momentum of inertia, B is rotation constant, J is the rotational quantum number.

For a non-rigid rotor, if we adopt Morse potential (where D is the dissociation energy of the molecule, r_e is equilibrium distance between nuclei, a is a constant) for low vibration states with r ~ r_e, the level energy containing centrifugal stretching is

Here, J and v are rotation and vibration quantum numbers, subscript e means quantities when atoms are in equilibrium position, and

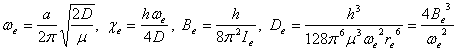
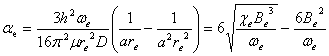
Here, μ=m₁m₂/(m₁+m₂) is the reduced mass the two nuclei m₁ and m₂.

A more appropriate solution for any potential function that can be expanded as a series of power of (r-r_e) in the neighborhood of the potential minimum is the Dunham’s solution:

Here, l and j are summation indices, Y_lj are coefficients depending on molecular constants. In the case of B_e/ω_e<<1 (say, for molecules not very light, e.g., the molecule H₂ is a bad case), one has the approximate relations:

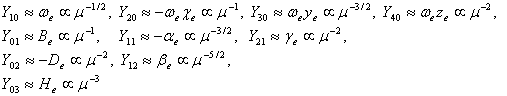
(Note: Part of the scaling relation is from the documents of NIST diatomic spectral database.) The above scaling relations with the reduced mass μ of the molecule are very useful to approximately calculate the energy levels of rare isotopic diatomic molecules from their main isotope, because for many molecules, the only significant difference among isotopomers is nothing but the reduced mass.

When electronic orbital angular momentum and/or spin exist, the energy level structure is determined by the angular momentum coupling schemes. There are four typical coupling schemes: the Hund’s cases (a,b,c,d) (see Appendix B for details). The most useful one is the Hund’s case (b) coupling, the case (a) occurs sometime, while the cases (c) and (d) are very rare.

For Hund’s case (a) coupling, the energy level is

Here B_v is the rotation constant corresponding to vibrational state v, A is also a rotation constant that is usually much larger than B_v. Ω is the quantum number for the projection of J along the molecular axis.

For Hund’s case (b) coupling, the energy level is

….

For Hund’s case (c) coupling is identical to that of case (a). For Hund’s case (d), the energy level is

For fine and hyper fine splitting, the energy levels are… (????)

What is the role of parity in the energy level formula? (For example, the energy levels of SiC are different for different parities.)

With external magnetic field, ……(Zeeman effects)

Statistic weight

For pure rotational levels: g_J = 2J+1

The only angular momentum not included in the quantum number J is nuclear spin. For rotational levels with non-zero nuclear spins (hyperfine structure splitting), the statistic weight for a pure hyperfine splitting level is

,

while that for a pure rotational level (not differentiating hyperfine components) is:

.

It’s not difficult to verify the second equality using the quantum angular momentum coupling rule:.

Selection rules

Selection rules for electric dipole transitions in the absence of external field: (from NIST diatomic spectra database documents)

For X¹Σ molecules:

For X³Σ molecules: (e.g., O₂, SO)

Actually is also allowed for intermediate coupling case,

for magnetic dipole transitions:

For X²Π molecules:(Hund’s case a, e.g., NO)

Electric dipole moment for transitions

For the case of L=0, S=0 (say, ¹Σ state),

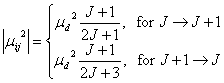
Here, μ_d is the permanent electric dipole moment of the molecule. The line strength thus is

For the case of L>0 (nonzero electronic orbit momentum), the molecule can be treated in analogue of symmetric top, so that the rotational line strength for Hund’s case (a) coupling is

,

in which Λ is the projection of L along the molecular axis. For the Hund’s case (b), the line strength is

….??????? ??????

In the case of fine structure splitting (S>0), the total of line strength of all fine structure lines just equals to the rotational line strength given by above formulas with the quantum number J replaced by N, while the relative intensity (RI) of fine structure lines should be determined by the quantum angular momentum coupling formula (see details on this in Appendix A). Eventually, the line strength for a single fine structure transition is simply S(N,J) = S(N) * RI.
Linear molecules

(Most contents from chapter 2 of Townes C.H. and Schawlow A.L., Microwave Spectroscopy, New York: McGraw-Hill, 1955)

Quantum numbers

For the case with L=0,S=0,I_i=0: J, ν₁,…, l (J=N)

with L=0,S>0,I_i=0: N, ν₁,…, l, J

with L=0,S=0,I_i>0: J, ν₁,…, l, F₁,…, I_tot, F (J=N)

with L>0,S>0,I_i>0: N, ν₁,…, l, J, F₁,…, I_tot, F (Hund’s case b)

with L>0,S>0,I_i=0: Ω, Λ, J (Hund’s case a, e.g., X²Π state molecules)

with L>0,S>0,I_i=0: Ω, Λ, J, F₁,…, I_tot, F (Hund’s case a)

l Here, N, ν₁,…, l, Ω, Λ are called principal quantum numbers, J, F₁,…, I_tot, F are called spin involved quantum numbers. For molecules with identical nuclei, the sign of Λ may reflect parity. F₁,… are needed only when any nuclei have non-zero spin. I_tot is needed when two spins couple with each other before being coupled to the total angular momentum.

l There are two ways to specify the vibration quantum numbers ν₁,… values: 1) list all ν₁^l values, with non-zero l as superscript: ν₁, ν₂^l, ν₃,… (suitable for small molecules, e.g., 01¹0 state of CO₂); 2) only specify the non-zero ν₁^l values (suitable for large molecules, e.g., ν₇=1¹,N=23,J=47/2 of C₄H).

Energy level

With centrifugal stretching effects, energy level of a linear molecule is:

with ,

where α_i is rotational constants that reflect the change of B from its equilibrium value B_e due to ith vibration mode. d_i is the degeneracy of the ith vibration mode, or the number of degenerate modes with the same α_i, D is the centrifugal stretching coefficient.

For a degenerate excited bending mode, with the l-doubling considered, the energy level for the case of |l|=1 is

with

Here, ν_k is the zero energy of the ground level of the degenerate vibration mode, l is the bending vibration angular momentum quantum number, q_l is the l-doubling coefficient. For higher excited bending modes with |l|>1, the l-doubling is usually very small (not important for mm wavelength).

With external magnetic field, ……(Zeeman effects)

Statistic weight

For pure rotational levels: g_J = 2J+1

As long as the molecule is not in the degenerate excited bending mode, the only angular momentum not included in the quantum number J is nuclear spin. For rotational levels with non-zero nuclear spins (hyperfine structure splitting), the spin statistics is (2I+1). Therefore, the statistic weight of a hyperfine is: g_F = (2I+1)(2J+1) =2F+1.

Selection rules

Selection rules for electric dipole transitions in the absence of external field:

Electric dipole moment for transitions

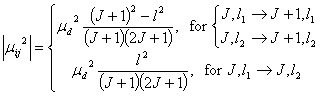
Here, μ_d is the permanent dipole moment of the molecule and l₁ and l₂ represent the two l-doubled sublevels with lower and higher energy, respectively. One can easily see that for ground vibrational level with l=0, the formula is identical to that of the diatomic molecule. The line strength thus is

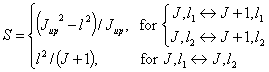
One can see the similarity of above formula with the dipole moment of symmetric top. Actually the excited bending mode of linear molecule can be considered as an asymmetric top with slight asymmetry. The quantum numbers of the excited bending mode can be analogously written in the form of asymmetrical top as:

For the higher l-doubling level: J,l => J_|l|,J+1-|l|, and

For the lower l-doubling level: J,l => J_|l|,J-|l|

Then, in the slight asymmetry limit, the dipole formula is the same as that of a symmetric top.
Symmetric top

(Most contents from chapter 3 of Townes C.H. and Schawlow A.L., Microwave Spectroscopy, New York: McGraw-Hill, 1955)

Energy level

For a rigid symmetric top, the energy level is

Here C is the rotation constant along the symmetry axis, B perpendicular to the axis. With centrifugal stretching considered, the energy level is

For a rigid symmetric top with l-type doubling, the energy level is

Here, |ς| ≤ 1 is a coefficient describing how well the bending motion is perpendicular to the molecular axis C, with a value of 1 for the entirely perpendicular case.

With external magnetic field, ……(Zeeman effects)

Statistic weight

Usually, a symmetric top has at least 3-fold of symmetry (except the rear case of accidental symmetric top made from linear molecules). The statistic weight of a pure rotational energy level is g_J = 2J+1. With hyperfine structure splitting, the statistic weight then becomes g_F = 2F+1. For a molecular energy level with hyperfine structure splitting but with the hyperfine structure transitions unresolved, the statistic weight of such an unresolved rotational level is composed of two independent parts: pure rotational levels weight g_J and the spin statistics weight S(J,K). Then, the total statistic weight of the unresolved rotational level is the multiplication of the two parts:

The spin statistic weight for any given rotational level J of a 3-fold symmetric top is

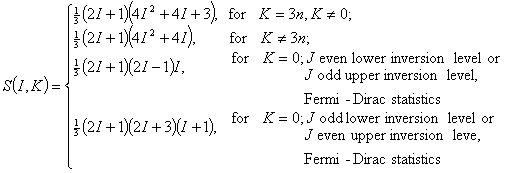
in which I is total nuclear spin quantum number, n is a non-negative integer. (A nucleus with odd mass number usually has half integer spin and so obeys Fermi-Dirac statistics, say, exchange of any pair of such identical fermion nuclei results in the reverse of the sign of the molecular wave function. In this case, one says the total wave function of the molecule is anti-symmetric w.r.t. the exchange of the identical nuclei. Oppositely, a nucleus with even mass number usually has integer spin and so obeys Bose-Einstein statistics, say, exchange of any pair of such identical boson nuclei will result in completely the same molecular wave function. One says that the total wave function of the molecule is symmetric w.r.t. the exchange of identical nuclei.)

Similarly, for a 4-fold symmetric top molecule, the spin statistic weight is

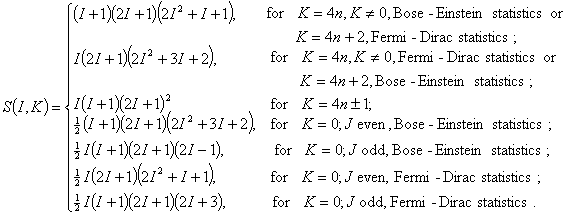
Selection rules

Selection rules for electric dipole transitions in the absence of external field:

Electric dipole moment for transitions

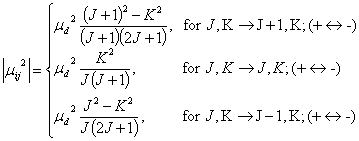
Here, μ_d is the permanent dipole moment of the molecule. The J,K – J,K transition is the inversion transition of molecules like NH₃. One can easily see that for the limit case of K=0, the formula is identical to that of the diatomic molecule. The line strength thus is

?????

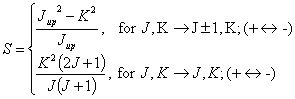One can easily see that the line strength is identical for both emission and absorption. When (hyper-)fine structure splitting exists, the sum of line strength of all (hyper-)fine lines should be just equal to the rotational line strength calculated by above formulas. The relative intensity (RI) of each (hyper-)fine lines should be computed according to quantum angular momentum coupling formulation (see more details in Appendix A).

Asymmetric top

(Most contents from chapter 4 of Townes C.H. and Schawlow A.L., Microwave Spectroscopy, New York: McGraw-Hill, 1955)

Energy level

For a rigid asymmetric top that is merely slightly asymmetric, the level energy is

For prolate top:

For oblate top:

in which A, B and C are rotation constants along the three molecular axes and the convention of A>B>C is assumed, and

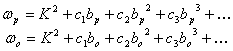
Here,

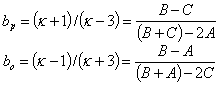
are asymmetry parameters for prolate and oblate tops, respectively, with

being King’s asymmetry parameter.

For a highly asymmetric rigid top, the energy level is

with only a function of κ. A list of can be found in G. Erlandsson, (1954, Arkiv For Fysik, 8, 189). There is a useful relationship: .

For a non-rigid asymmetric top, the energy level including centrifugal stretching effects is

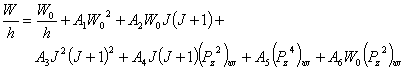
Here, A_i’s are constants, W₀ is the rigid asymmetric top level energy given above,

with I_zz being the moment of inertia matrix element. In the limit cases of symmetric top or near symmetric top, one has

Statistic weight

For pure rotational levels g_J = 2J+1. If hyperfine structure splitting exists, each hyperfine structure level has statistic weight of g_F = 2F+1.

Selection rules

Selection rules for electric dipole transitions in the absence of external field:

Electric dipole moment for transitions

Here, μ_x is the permanent dipole moment of the molecule while x is the axis along which the dipole moment is non-zero and so is responsible for allowed transitions. The calculation of the term is complex. A table of the values of this term is given for different x, J, K₁, K₂, κ and transition types P, Q, and R in the Appendix V of the book by Townes and Schawlow (1955). The transition types P, Q and R are corresponding to ΔJ = -1, 0, and 1, respectively. Here are several useful relations:

Here x and x’ are the ones with the largest and smallest rotation constant (or momentum of inertia) among the three molecular axes. So the second formula means the change from prolate top base functions to oblate top ones, or vise versa.

For slightly symmetric tops (with parameter κ close to 1 or -1), the line strength is very close to that of symmetric top by taking Ka as K. One of the good examples of such slightly asymmetric top is SiCC and its isotopologues.

Appendix A

Relative intensity (RI) of (hyper-)fine structure lines

(from notes by Dr. Dinh-Van-Trung)

The relative intensity of fine or hyperfine structure lines is determined by the quantum mechanic angular momentum coupling theory. First of all, let’s consider a pure rotational transition from any level J to any level J’, the electric dipole moment of the transition is

.

Here, M is the projection quantum number of J along any axis. Therefore, only transition from J to J’=J-1 has nonzero dipole (allowed). The dipole moment of a transition from one degenerate sublevel of J to all degenerate sublevels of J’ is

.

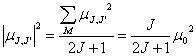Hence, line strength for a pure rotation transition is

Now, let’s consider a Hund’s case (b) coupling of rotational angular momentum N, electronic spin S and nuclear spin I. N couples with S to produce angular momentum J, then J couples with I to produce F. This can be expressed using the Dirak bracket as

.

Then, the transition dipole moment that is used in the formula of Einstein A coefficient is

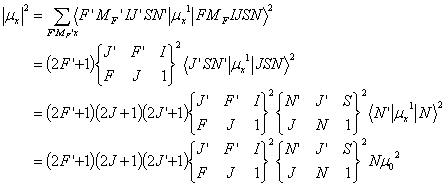
Thus the line strength S can be derived from the relationship:

Here the symbol {} is the so-called 6-j symbol. The constant “1” in the right bottom corner means that we are calculating electric dipole transitions. The formulas to calculate 6-j symbols are

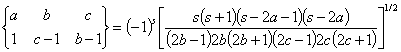
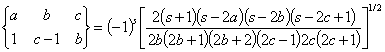
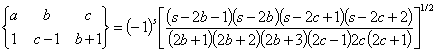
where s = a+b+c. Following property of the 6-j symbol is important for its implimentation: exchange of any two columns or exchange of two rows of any two columns doesn’t change the value. There are more 6-j formulas for other types of transitions (e.g., quadrupole transtions).
Appendix B

The four Hund’s cases for electronic angular momentum coupling

The angular momenta need to couple with each other because they exert torque on each other, so that some of the momenta have fast precession around other momenta or axes. The fast precession of momenta makes the momenta not conservative any more. But the projection of the fast precession momenta along their precession axes might be still conservative and so can be used to tag the energy levels of the molecule. For a linear molecule with electronic orbital momenta l_i and spins s_i, there are four types of most possible coupling cases: the Hund’s cases (a,b,c,d). In the four Hund’s cases, all individual orbital momenta and spins first couple with each other to form a total orbital momentum L and total spin S. Hund’s case (b) is the case found in most astro-molecules. Hund’s case (a) is much rarer, while Hund’s case (c) and (d) are not found yet.

Hund’s case (a) coupling: The coupling between the momenta L, S and the molecular axis is strong. Their projections on the axis are Λ and Σ, respectively. Λ and Σ add up to form Ω. Then Ω couples with couples with rotational angular momentum R to form the resultant angular momentum J. The coupling flow chart:

(1) L+axis=>Λ, S+axis=>Σ

(2) Λ+Σ=>Ω

(3) Ω+R=>J

Hund’s case (b) coupling: In this most possible case, the coupling between the momentum L and the molecular axis is still strong, but the coupling of S with the molecular axis is weak. So the projection of L along the axis, Λ, couples with rotational angular momentum R to form the resultant rotational angular momentum N. N directly couple with S to form the resultant angular momentum J. The coupling flow chart:

(1) L+axis=>Λ

(2) Λ+R=>N

(3) N+S=>J

Hund’s case (c) coupling: In this case, the direct coupling of momenta with molecular axis is weak, L and S first directly couple to resultant electronic angular momentum Jc, then Jc couple with axis with projection Ω. Ω further couples with R to form the resultant angular momentum J. The coupling flow chart:

(1) L+S=>Jc

(2) Jc+axis=>Ω

(3) Ω+R=>J

Hund’s case (d) coupling: In this case, the coupling of momenta with molecular axis is always very weak, so that L directly couples with R to form resultant angular N, then N directly couples with S to form the resultant angular momentum J. The coupling flow chart:

(1) L+R=>N

(2) N+S=>J