Typical basic parameters in interstellar space: Typical collision duration ~ 10^-14 s. (page 46) Typical collision cross section for neutrals ~ 10^-15 cm^2. (page 49) Typical collision rate coefficient between neutrals ~ 10^-11 cm^3s^-1. (page 49) Typical collision rate coefficient between neutral and electron ~ 10^-9 cm^3s^-1. (page 59) Typical collision rate coefficient between ion and electron ~ 10^-7 cm^3s^-1. (page 55) Typical spontaneous transition probability ~ 10^8 s^-1, so the corresponding life time in the excited state is 10^-8 s. (page 46) Electric interaction potential laws: (corresponding force laws can be derived by deviding 'r' from below formulas) (pages 49-50) charge-charge interaction potential ~ r^-2; (page 50, should it be r^-1?) charge-dipole interaction potential ~ r^-4;  dipole-dipole interaction potential ~ r^-3 (static value, if averaged over all possible orientations: ~r^-6) dipole-induced dipole interaction potential ~ r^-???; induced dipole-induced dipole interaction potential ~ r^-6 (the so-called dispersion force, page 49).
	Why molecules produced by late type stars are not the major source of interstellar molecular gas: Because the molecules from late type stars will be fast destroyed by interstellar UV photons when they travel to the outer part of the circumstellar envelope, while the size of the whole circumstellar envelope is tiny compared with the size of interstellar molecular clouds.
	Why dust grains produced by late type stars are not the major source of interstellar molecular gas: The dust grain formation rate in the whole Galaxy is 4x10^-10 Msun yr^-1 per square parsec of the galactic disk (calculated from typical mass loss rate and total number of late type stars). But this rate contributes less than 1% of the molecular content of diffuse clouds. Therefore, interstellar molecules should mainly come from synthesis, instead of grain breakdown.
	Basic formula in chemistry:  For reaction A+B -> C+D, if the reaction rate is k (cm^3s^-1), the product concentration change rates resulted from this reaction are         d n(C) /dt = d n(D) /dt = k * n(A) * n(B)
	Two-body chemical reaction is difficult, because the exccessive energy can not be carried away, the composite system is unstable and will break up very soon.
	In typical interstellar condition, three-body chemical reaction is also too slow, because the possibility of simultaneous three-body collisions is very low while the temporarily formed two-body system will break up before the third body arrives.
	Simple analysis in typical interstellar conditions showed that the reaction rates of hydrides should be much lower than that of the other reactions. Reactions of many other types in gas phase and on grain surface may play a role in interstellar clouds.
	Under interstellar conditions, exothermic reactions usually overtake endothermic reactions. The thermal property of a reaction can be judged by comparing the dissociation energies of the reactants and products.

 

Gas phase reactions (back to top)

	Cosmic ray ionization (representative rate coefficient: 10^-17 s^-1) (click to (un)fold contents) The foundamental issue of interstellar chemistry is the formation of hydrides. The reactions between H and C, N, O, ... are initiated by ionization of H atom by cosmic ray (c.r.):         H  + c.r. -> H+ + e        + c.r.         H2 + c.r. -> H2+ + e      + c.r.  (2%)         H2 + c.r. -> H+ + H + e + c.r. (88%)         H2 + c.r. -> 2H              + c.r. (10%) The followed reaction          H2+ + H2 -> H3+ + H  produces the important active proton supplier H3+ for many other reactions. Another important product of cosmic ray reaction is He+. Only low energy c.r. is important for cosmic ray reactions, because high energy c.r. has much smaller reaction cross section.  The cosmic ray reaction rate is unknown. It's usually taken as a free parameter. From known spectrum of higher energy c.r., the lower limit of the reactions reactioin rate is >= 10^-18 s^-1 per H atom; from the energy balance at the center of dark clouds where the cloud is heated by c.r. and cooled by CO emission, an upper limit of the reaction rate can be derived as <= 3x10^-17 s^-1 per H2 molecule. The canonical value is 6x10^-18 s^-1 per H atom.
	Ion-Molecule reactions (representative rate coefficient: 10^-9 cm^3s^-1) (click to (un)fold contents) For ion-molecule reactions in the form of          A+ + BC -> AB+ + C,  laboratory studies suggest that the majority of exothermic ion-molecule reactions (not all of them) have a reaction rate of the order of 10^-9 cm^3 s^-1 and largely independent of  temperatures (in the range of 300-1000 K). Although exact quantum mechanical calculations with Born-Oppenheimer approximation is possible, classical treatments also provide some insights. The classical theories that assume the reaction rate equals to collision rate can give good estimate of reaction rates but give no information about the products of the reactions.There are two cases in the classical treatments: Ion-nonpolar molecule reaction     Suppose the charge of the ion induces an electric dipole in the neutral molecule and the nuclei move in a potantial          V(r) = -alpha * e^2 / (2 r^4)  in which alpha is the average polarizability of the neutral molecule, e is the charge, and r is the ion-molecule distance, the collision cross section radius is          b0 = (4 e^2 alpha / mu / v^2)^(1/4)  in which mu is the reduced mass (1/mu = 1/mn + 1/mi, with neutral molecule mass mn and ion mass mi), v is the relative velocity of the two particles. The collision cross section is pi * b0^2 and the collision rate coefficient (= reaction rate) is         k = pi * b0^2 * v = 2pi * e * sqrt( alpha / mu ). This is the so-called Langevin value. It is independent of temperature (independent of collision velocity) and only slightly dependent on polarizability alpha and reduced mass mu. Because the polarizability of most interstellar molecules do not change much (about a factor of 5 of variation around 10^-24 cm^-3), it explains the fact that the majority of the measured ion-molecule reaction rates are of the same order of magnitude. Ion-polar molecule reaction     According to the so-called average dipole orientation (ADO) theory, the collision rate coefficient at thermal ion energies is         k(ADO) = [ 2pi * e / sqrt(mu) ] * [sqrt(alpha) + c * mu_D * sqrt(2 / pi / kT)], where mu_D is the permanent dipole of the polar molecule, T is the kinetic temperature, and c is a parameter between 0 and 1 (when T is fixed, c is only a function of mu_D/sqrt(alpha)). The value of k(ADO) only differs from the Langevin value by the second temperature dependent term. For a typical molecule with alpha = 5x10^-24 cm^-3, mu = 1 debye, c = 0.18 at 150 K, the temperature dependent term contributes 30% of the rate coefficient. Some typical reactions: (see the list of dissociation energy of some simple species here) Proton transfer:     AH+ + B -> BH+ + A generally occurs if it is exothermic; Proton abstraction:     A+ + H2 -> AH+ + H usually occurs with rate coefficients smaller than Langevin value; Proton ellimination:     A+ + BH -> AB + H+ apparantly does not occur; Condensation reaction: CH3+ + NH3 -> CH2NH2+ + H2 does not always occur, other exit channels are possible.
	Charge transfer reactions (representative rate coefficient: 10^-9 cm^3s^-1) (click to (un)fold contents) For a charge transfer reaction like         A+ + B -> A + B+ to take place, there are usually three conditions to fulfil:  (1) Rapid charge transfer condition. The collision duration t_col = a/v (a is a distance over which charge transfer is possible and v is the speed of impact) should be short enough to be at least comparable as the charge transfer time scale t_tr = h/|dE| (h is the Planck's constant and dE is the energy defect -- the difference between the ionization potentials of A and B). Therefore, in those regions where gas temperature is too low, no charge transfer will occur.  (why? Isn't it contrary to the Franck-Condon principle below?) They are called adiabatic regions. (2) Energy resonance condition. Because collision velocity v is usually small in interstellar conditions, condition (1) requires the energy defect dE to be small, i.e., A and B must have similar ionization potentials. This explains why the exothermic reactions         He+ + H2 -> He + H + H+         Ne+ + O2 -> Ne + O + O+ are very slow while the similar exothermic reaction         He+ + O2 ->  He + O + O+ is fast, because in the first two reactions, the ionization energy of He and Ne are very different from that of H2 and O2 respectively while in the third reaction, the ionization energy of He is close to that of O2. (3) Franck-Condon principle should be satisfied. When two molecules collide, the charge transfer from on molecule to the other can be considered as a transiton between two electronic states within the unstable two-molecule complex. Because electronic transition is much faster than the motion of nuclei, the nuclei should not move appreciably during the charge transfer. However, the electronic transition will change the potential of the complex and so the initial and final electronic states will usually be on different vibrational states. Then from a quatum mechanical point of view, it is naturally required that the initial and final vibrational states should share similar neuclei configurations, or in another word, the overlap integration of the initial and final neuclei wavefunctions should be large. Otherwise, the charge transfer may not occur. (See the Wiki entry for the Franck-Condon priciple in gas, liquid and solid.) For larger systems such as polyatomic molecules, these conditions become not so rigid. The energy resonance requirement will usually be met because the density of states per unit energy is large for complex systems. The Franck-Condon priciple will be broken due to the distortion of the complex molecule (self-adaptively changing the vibrational potential) during the interaction.
	Radiative association (representative rate coefficient: 10^-17 cm^3s^-1 for diatomic and 10^-9 cm^3s^-1 for polyatomic) (click to (un)fold contents) For a radiative association reaction like         A + B -> AB + h*nu, the electrical interaction between the two approching partical A and B can be either always repulsive or far-distance attractive. In the case of repulsive potential, the two particles can not easily approch close enough to share electron clouds, hence no reaction may occur in interstellar space. In the case of far-distance attractive potential (e.g, the Morse potential), shared electron cloud can temporarily form and then, the complex can be stabilized by releasing exccessive energy in the form of a photon whose energy h*nu is no less than the collision energy. A crude estimate of diatomic radiative association rate k_RA: The duration of a typical collision event is about 10^-14 s, the typical transition time of a strong electronic transition is 10^-8 s (for a Einstein constant of 10^8 s^-1), hence the probability for the stabilization transition to occur is 10^-6 per collision. Furthermore, the typical collision rate coefficient for neutrals is on the order of 10^-11 cm^3s^-1. Therefore, a typical value of k_RA = 10^-17 cm^3s^-1. When at least one of the reactants is a molecule, the collision energy will be shared by a number of bonds, the collision time may considerably increase because the chance to have enough energy in a single bond to get the molecule dissociated is lower. Consequently, the radiative association rate k_RA of large molecules is close to collision rate while k_RA of smaller molecules is between the collision rate and diatomic value. The temperature dependence of radiative association rates is unclear yet. But evidence from ternary reactions suggests that k_RA could be higher at lower temperature.
	Neutral exchanges (representative rate coefficient: 10^-11 cm^3s^-1) (click to (un)fold contents) For a neutral exchange reaction like         A + BC -> AB + C, experiments showed that it's reaction rate sometimes sensitively depends on temperture, sometimes does not. To constrain the reaction rate coefficient, we can follow 2 steps. First step, we can assume the reaction rate is equal to collision rate, then the reaction rate coefficient is         k ~ sqrt(T/mu). However, whether every collision event results in a neutral exchange depends on the interaction potential of the reactants and products. When polar molecules are involved in the reaction, it will induce an additional electric dipole in the other molecules to strengthen the interaction. When only non-polar molecules are involved, they can also induce a weaker instananeous dipole in each other. When averaged over all instananeous configurations of electrons, this instananeous dipole interaction is just the so-called dispersion force. With the Born-Oppenheimer approximation (electrons adapt themselves very fast, neuclei move on a series of average potential supersurfaces), the interaction potential supersurfaces (dipole-dipole, or dipole-induced dipole, or induced dipole-induced dipole) are only functions of distances between neuclei pairs (3N-6 independent distances). For some molecules, the initial location on the potential supersurface is lower than the final location, the reaction is endothermic and usually impossible in interstellar environment. For exothermic neutral exchange reactions, sometimes there exist a potential barrier to overcome to activiate the reactions (e.g., some reactions of O and N atoms), while for some other molecules, the potential barrier is very small or negligible (e.g., many reactions of C atoms). The behavier of this potential barrier to neutral exchange reactions can be described as         k ~ exp(-q/kT) where q is the potential barrier. Finally, we can obtain a general formula for the exthothermic neutral exchange reaction rate coefficients by combining above two formulas:         k = A * sqrt(T) * exp(-q/kT) where A is a constant to be determined for individual reactions by theoretical calculations or experiment measurements.
	Radiative recombination (representative rate coefficient: 10^-12 cm^3s^-1)  (click to (un)fold contents) In a radiative recombination reaction like         X+ + e -> X + h*nu, the surplus energy is released as radiation. In diffuse interstellar clouds, the main ions are C+ (from photoionization of C atoms) and H+ (from cosmic ray ionization of H atoms). We consider mainly two kinds of recombination reactions: Single electron recombination    A crude classical estimate of the reaction rate coefficient is as follow: the typical collision rate coefficient between an ion and an electron is roughly 10^-7 cm^3s^-1, the probability of radiating during the collision is 10^-5 to 10^-6 per collision, therefore, the radiative recombination rate coefficient is          k_RR ~ 10^-12 to 10^-13 cm^3s^-1. The value of k_RR may depends on temperature as ~1/sqrt(T), but deviation is also seen from time to time. The recombined electron has more chance to reside in the lowest energy level, but also possible to reside in excited level and then cascade downward to produce recombination lines. Dielectric recombination    If the ion has at least one electron, another possible process is to exite the orbiting electron by the incident electron so as to produce a doubly excited atom:         X+ + e -> X** Such doubly excited atom is unstable and will either be autoionized:         X** -> X+ + e  or emit a photon to stabilize the recombination:         X** -> X + h*nu. The lifetime of X** against autoionization is <= 10^-13 s and against radiatioin is <= 10^-8 s, hence, as the single electron recombination case, only a small fraction of them will end up with radiative recombination. Such dielectronic recombination is possible only when the incident electron has an energy higher than the first allowed transition in the atom (> 10 eV). Since the fraction of such high energy electrons is usually small, unless the temperature is as high as 10^5 K, the dielectric recombination is unimportant in interstellar clouds.
	Dissociative recombination (representative rate coefficient: 10^-6 cm^3s^-1) (click to (un)fold contents) For a dissociative recombination reaction like         AB+ + e -> A + B, it usually proceeds in two steps:  1) form the incident electron excite another electron of the ion and itself resides in another excited state:         AB+ + e -> AB**;  2) The unstable excited molecule AB** dissociate into two particles:         AB** -> A + B. The basic requirement: there should be one of the many states of AB lying close to the initial state of AB+. Measurements of the reaction rate coefficient k_DR showed that it usually very large and range from 10^-7 to 10^-6 cm^3s^-1, with a temperature dependence of ~T^p, with p ~ 1/2. Two notable exceptions to the large k_DR are H2+ and He2+, because the neutral H2 and He2 do not have the required repulsive potential energy curves.
	Negative ion reactions (representative rate coefficient: 10^-9 cm^3s^-1) (click to (un)fold contents) Negative ions in interstellar clouds can be formed through radiative attachment reaction:         X + e -> X- + h*nu, where X is neutral atom or molecule with a positive electron affinity. The radiative attachment rate coefficient should be much smaller than that of recombination between positive ion and electron, because the electron-neutral interaction is much weaker. With typical collision rate coefficient of 10^-9 cm^3s^-1, typical collision duration of 10^-14 and typical spontaneous transition lifetime of 10^-8 s, a rough estimate of the radiative attachment rate coefficient is 10^-15 cm^3s^-1. The negative ions are readily to be destroyed by photodetachment reaction:         X- + h*nu -> X + e. Because the interaction between the electron and atom is weak, the photodetachment cross section should be large. Under the typical interstellar radiation with mean flux of 10^7 photons cm^-2s^-1nm^-1 within 0~10^3 nm, the mean cross section of H- is 2x10^-17 cm^2, which result in a photodetachment rate coefficient of about 10^7 s^-1. The rate coefficient of other negative ions should be similar as this, because it is not strongly related to the nature of X itself. Alternatively, the negative ions may reaction with other neutrals through associative detachment reaction:         X- + Y -> XY + e, or react with positive ion through mutual neutralization reaction:         X- + Z+ -> X + Z. If the associative detachment reaction is exothermic, it should proceed with the typical collision rate coefficient 10^-9 cm^3s^-1, because after the collision, the autoionization time scale of 10^-14 s is much shorter than neuclei motion timescale. Experiments show that if X- and Y are atoms, all exothermic reactions are fast, while this is not true if X- or Y is molecule.     The mutual neutralization is dominated by long range Coulomb forces and so has large cross section. Laboratory measurements and theory  show that the rate coefficient has a T^(-1/2) dependence at low temperature, which indicates that it is more efficent at lower temperature. Typical mutual neutralization rate coefficent is 10^-6T^(-1/2) cm^3s^-1. The contribution of negative ion reactions to the interstellar chemistry is usually much smaller than positive ion reactions. But in some situation, it can be fast. For example, it is the fastest gas phase route to form H2 (but not competative with grain surface reactions).

	The interstellar radiation flux F(E) measured in relatively transparent regions of the interstellar medium is well approximated as         F(E) = 1.658x10^6 E - 2.152x10^5 E^2 + 6.919x10^3 E^3      photons cm^-2 s^-1 ster^-1 eV^-1 where E is the photon energy in eV. This expression is valid for 5 eV <= E <= 13.6 eV. The photons more energetic than 13.6 eV have been absorbed by the most abundant element -- H atoms.
	The interstellar radiation flux F(E) in dense clouds will be different from this due to absorption by dust and molecular lines.
	The ionization absorption continuum of H2 is < 1109 A; that of C atoms is < 1101 A.
	Photodissociation rate beta0 of a molecule can be calculated through         beta0 = 4*PI * INT^13.595_0{ F(E) * sigma_pd(E) dE } where sigma_pd(E) is the photodissociation cross section. Typical values of beta0 lies between 10^-9 and 10^-11 s^-1.
	Because photoionization is active only at short wavelength, dust opacity play an important role in the ionization balance.

	Spatial density of grains  (click to (un)fold contents) Two types of interstellar dust grains: large grains with rho = 2* PI*a/lambda >>1 and small grains with rho <=1 (here a is grain radius and lambda is the considered radiation wavelength). From the measurement of interstellar extinction A_nu, we have Q_ext*PI*a^2*n_g = 6.0x10^-22 cm^-1, where Q_ext is the extinction efficiency factor calculated from Mie scattering theory and n_g is the number density of grains. An important factor for chemistry is the grain surface area per H atom per cm^3:         epsilon = PI*a^2*ng/<n> = 2.5x10^-22 cm^2  (for large grains)         epsilon = PI*a^2*ng/<n> = 1.8x10^-22 cm^2  (for small grains)         epsilon = PI*a^2*ng/<n> = 2.1x10^-22 cm^2  (on average)
	The nature of grains  (click to (un)fold contents) Dangling radicals can appear on the surface of grains, e.g., -CH, -OH, -NH2, -HCO on amorphous carbon dust grain surface and -OH on silicates surface.  The bond of some of these radicals can be seen through resonance dust emission features in infrared, e.g., the 3.3, 3.4, 6.2, 7.7, 8.6 and 11.3 um broad dust emission features.
	Formation of molecules on passive grain surface  (click to (un)fold contents) Atoms can be adsorbed on the grain surfaces due to adsorption potential wells. Grain surface can be devided into two categories: passive and active surfaces. Passive grain surface is only active in physisoption (adsorption due to weak van der Waals forces), while active grain surface is active in chemisorption (adsorption due to formation of chemical bonds, either covalent or ionic). The typical adsorption potential well is ~ 1 eV for active grain surface and only ~ 10^-2 eV for passive grain surface. Sticking probability of atoms on active grain surface is almost equal to collision probability, while that on passive grain surface is several orders of magnitude lower. If the adsorption energy is D or in unit of K as D/k, the lifetime of an adsorbed particle against evaporation at the grain temperature T_g is, classically,          t = (1/nu) * exp(D/kT_g) where nu is the characteristic vibrational frequency of the adsorbed atom in the adsorption potential well D. If the lifetime is too short, the particle may have no time to react with other particles before evaporation. On a passive grain surface, adsorbed atoms may move on the surface due to residule kinetic energy. However, under all likely interstellar conditions, only light atoms like H are fairly mobile on grain surface, while (adsorbed) heavy atoms such as O and C are relatively immobile and will tend to be incorporated into hydrides. From the quantum mechanical point of view, mainly light atoms like H can easily tunel through energy barrier of surface reaction, therefore, grain reaction products are mainly hydrides like CH4, NH3 and H2O. Table. Formation rates (cm^-3s^-1) due to reactions on passive grain surfaces predicted for some molecules in low and high density  clouds. (under arbitrary assumptions) Low density (n=100 cm^-3) High density (n=2x10^4 cm^-3) CH4 5.8x10^-17 1.1x10^-15 H2O 5.8x10^-17 6.6x10^-15 NH3 1.4x10^-17 4.0x10^-16 C2 4.9x10^-21 1.1x10^-13 O2 4.9x10^-21 1.8x10^-14 N2 3.1x10^-22 1.0x10^-15 CO 4.9x10^-21 4.5x10^-14 CN 1.2x10^-21 1.1x10^-14 NO 1.2x10^-21 4.4x10^-15 Reaction rate equations for passive surface reactions: Let Rx be the number of atoms X on a grain surface, and Rxy the number of molecules XY on the grain. Then, with assumption that each XY will be ejected into gas phase once it is formed on the grain surface, the change rate of these numbers are          d Rx / dt = beta_x * n_x - SUM_Y{Rx * Ry * gamma_xy},         d Rxy /dt = Rx * Ry * gamma_xy - SUM_W{Rw * Rxy * gamma_w,xy} where gamma_xy is the rate coefficient (s^-1) for the surface reaction of X and Y, and beta_x*n_x is the rate at which atom X is being adsorbed onto the grain (n_x is gas phase number density of atom X and beta_x is the adsorption rate coefficient in cm^-3s^-1). The atom W represents other atoms that react with molecule XY to reduce the number of the XY on the grain surface. In a classical treatment, the surface reaction rate coefficient can be written as         gamma_xy = v_xy * l_xy / Q where v_xy is relative velocity of the reactants pair X and Y, l_xy is the reaction distance, and Q is the grain surface area (=4*PI*a^2 for spherical a grain). Eventually, the formation rate of the molecule XY in a dusty medium is          d n_xy / dt = n_g * SUM_X,Y{Rx * Ry * gamma_xy} where n_g is the number density of grains.
	Formation of molecules on active grain surface  (click to (un)fold contents) On active grain surface, impinging atoms form strong chemical bond with surface ions. Such actions usually only proceed along specific pathways, depending on the chemical properties of the surface and the impinging atoms. The chemical property of the two classes of grains, oxygen and carbon grains, are different. The active ions are usually O2- on oxygen rich grain surface and C+ on carbon rich grain surface. Therefore, oxygen rich surface is usually oxidizing agent, while carbon rich surface is usually reducing agent. However, other kinds of defect can also be active desorption sites, e.g., vacancies, electrons in vacancies, other ions that have replaced O2- or C+. Photoelectric emission also creates defects on the grain surface. An adsorbed atom first form a complex with surface ions, then the complex will be either stabilized by transfer of excess energy to the grain surface or dissociated. If dissociated, the particle returned to gas can either be a neutral atom or a neutral molecule (but can not be a ion because otherwise the strong electric force will prevent the dissociation). Element depletion pattern (depletion degrees of different elements) in molecular clouds may provide information on the grain surface reactions. It was found that although different clouds may show different depletion patterns, a common trend is the higher depletion of elements with lower ionization potential. Element depletion is usually defined as          Dx = log10(Nx/N_H) - log10(Nx/H_H)_sun. Catalysis on grain surface is also possible. For example, the formation of oxygen-rich molecules H2CO and H2O in the carbon star envelope around IRC +10216 is believed to be catalyzed by dust grains.
	Actually, the same dust grain surface can be active to some atoms or molecules but passive for the other, depending on the chemical properties of the surface.
	Chemical reactions on the surface of small dust grains may raise the temperature of the grain, because the heat capacity of small grains is usually small while released chemical energy is huge. Assuming the bond formation releases energy of E_bond and the heat capacity of the grain is Cv(T), then         E_bond = INT_Ti^Tf{ Cv(T) dT } where Tf and Ti are final and initial grain temperatures and the heat capacity is         Cv(T) = ( 48 * PI^5 * a^3 / 15 ) * ( rho * R / M ) * (T / thetaD)^3 in which a is the grain radius, rho is the grain density, R is the molar gas constant, M is the molecular weight of the grain material, and thetaD is the Debye temperature of the grain material. This formula is valid when T < 0.5 thetaD. Integration of the formulae gives         Tf = (4* E_bond * / Cv' + Ti^4)^(1/4). Here Cv' = Cv(T)/T^3 is a quantity unrelated to T. Simple calculations show that molecule formation on small grain surface produces significant grain heating.

	The abundance of H2 is usually determined through observation of its UV absorption line or the weakness of 21cm emission of H atom. In some hot sources such as shock regions, it is also possible to detect the quadrupole vibrational transitions. Dipole transitions are forbiden.
	H2 abundance is usually expressed as f = 2n(H2) / [n(H)+2n(H2)]. The measured values of f in interstellar clouds is found to be either very high in dense clouds or very low in inter-cloud regions.
	Formation of H2 in diffuse clouds: radiative association of two H atoms is too slow, because the collision time is too short; radiative association of H and H+ is also too slow, because H+ abundance is not high enough; negative ion reaction between H and H- is also too slow with such low temperature (it could be important in hot regions because the formation rate of H- is proportional to T);  three body reaction of H atoms is too slow; only dust grain surface reaction can be fast enough to compete with the fast photodissociation processes.
	If all H2 molecules are formed on grain surface, the formation rate coefficient can be estimated from observed H density as R = 3x10^-17 cm^-3 s^-1. The formation rate is R*n*n(H), where n = n(H) + 2n(H2) and R is in cm^3s^-1. Then the rate of change of H2 density is      dn(H2)/dt = R*n*n(H) - beta(r)*n(H2) where beta(r) is the photodissociation rate at location r.
	The sythesis of H2 on grain surface:          H + H + grain => H2 + grain with rate constant of          k = 1/2 pi * a^2 * v * P  [cm^3s^-1] where P the probability that an H atom colliding with a grain is adsorbed and reacts for form H2. The formation rate of H2 is k*n(H)*n_g.  The weak physisorption sites of H on the grain surface are NOT the main sites of H2 sythesis. Why? The weak adsoprtion time scale is         t_w = (1/nu) exp(D_w/kT_g), where it is assumed that the probability to overcome an energy barrier of height D_w at temperature T_g is exp(-D_w/kT_g) and that the H atom has nu opportunities per second to overcome such a barrier. While the collision time scale of H atoms with grains is         t_k = 1 / [ksi * pi * a^2 * v * n(H)], where ksi is the probability of a colliding H atom to be physically adsorbed on the grain surface, a is the grain radius, v is the relative speed of collision. Only when t_w > t_k, the H2 sythesis will be possible. However, this require the H2 production rate R to be sinsitive to grain temperature T_g, which was not observed. The strong chemisorption sites of H on the grain surface are the main sites of H2 systhesis. Why? An H atom will first be adsorbed at weak physisorption sites, then it migrates around to a strong chemisorption site or meet another H atom to form H2. The grain surface is composed of many small lattices separated by potential barriers. The probability for the H atom to tunel through one of such barrier is         rho = 1 + [D_w^2 * sinh(beta)^2 * Delta / 4E(D_w-E)] ^-1, where beta = hbar * sqrt[2m(D_w-E)]. The timescale for the tunneling is          t_h = 1/(rho*nu) with E = h*nu. Then the time scale for a physisorbed H to relocate to a strong chemisorption site will be         t_m = lambda * t_h   (via diffusion) or         t_m = lambda^2 * t_h (via random walk), where lambda is the number of lattice spacings from the initial to the final site. With typical values (D_w/k = 400K, nu = 10^12 Hz, m = 1.6x10^-27kg, Delta = 10^-10m, lambda = 200), the condition for a success relocation of H atom to a strong adsorption site is t_m = t_w, which results in a grain temerature of T_g = 32.8K (diffusion) or 22.9K (random walk). This reasonable grain temperature demonstrate that the migration of H atoms on the grain surface is efficient.     The H+H reaction at enhanced binding sites is exothermic, with an activiation energy of 5% of the bond between the H atom and grain surface. The relatively large activiation energy can be compensated by the relatively long residence time of the two H atoms at the chemisorption sites. Therefore, the reaction rates is eventually mainly controlled by arrival rate of H atoms at the grain surface. The product H2 molecule will evaporated in to gas rapid because the binding energy of an H2 molecule on the grain surface is much smaller than that of an H atom. The newly formed H2 molecules may be in excited rotational-vibrational states.
	Radiation from H2 molecules: UV fluorescence H2 can be pumped by interstellar UV radiation. A rough estimate shows that it can be as bright as the scattering of the interstellar UV radiation by dust grains. Because the H2 molecules are expected to be in vibrationally excited states, IR fluorescence should be produced. However, if the production, photodissociation and the radiative relaxation of the H2 molecules are all in equilibrium, the contribution of H2 fluorescence emission from H2 formation could be negligible, because the relaxation rate is very large, so that the equilibrium population will be very low, while observed H2 emission indicate a significant of exited population.
	H2 in dark clouds Dark clouds can be defined as those condensitions where light within the wavelength range that leads to photodissociation of H2 is excluded. Such clouds typically have H2 density n > 100 cm^-3 and H2 column density > 10^21 cm^-2. In dark clouds, H2 molecules are mainly formed on grains and destroyed by reactions initiated by cosmic ray reactions (with c.r., e, H2+, He+). Because the formation and destruction rates are both proportional to the density of H atoms, the equilibrium results in a density of atomic H in the H2 clouds: n(H) ~ 1 cm^-3, and an ionization fraction of n(e)/n ~ 10^-6 /sqrt(n).

	Difficulty of chemistry modelling lie in: 1) many reaction rates are estimated and so uncertain; 2) grain surface reaction rate is even more uncertain.
	Some parameters to be obtained or specified in the modelling: density, temperature, interstellar radiation field, grain scattering parameters, cosmic ray ionization rate, relative abundance of elements, cloud size and shape.
	A self consistant model should treat the thermal and pressure equilirium of the clouds simultaneously. But this was rarely attempted because the lack of understanding to heating rate.
	Time dependent and equilibrium chemistry Where does equilibrium chemistry can be expected? Here are the estimates of several typical cases: In diffuse clouds, assuming the production rate F_x of a species X is constant and X is mainly destroyed by photons at a rate of beta_x, the rate equation is         d/dt n_x = F_x - beta_x * n_x. The equilibrium value of n_x = F_x / beta_x will be reached on a time scale of 1/beta_x, i.e., the photondestruction time. This is typically several 10^3 years, much shorter than the lifetime of diffuse clouds. Therefore, such reactions are readily in equilibrium. However, some slow reactions such as atom exchange reactions could take longer time (~10^5 years), but is usually still shorter than the lifetime of the clouds. In dense clouds, molecules are usually destroyed by reactions with ions. For example, CO is mainly destroyed by He+ and the typical destruction time scale is several million years. This is comparable to the cloud lifetime, therefore, chemistry equilibrium can be roughly established. In many other situations, such as shock waves and circumstellar envelopes, time dependent chemistry is expected. In general, all reactions other than cosmic ray ionization, photodissociation, and photoionization, can be regarded as two body reactions. Grain suface reactions can be equivalently considered as two body reactions as well. The rate equation for molecule X formed by various reacting pairs A and B,         A + B => X + Y (kAB) and destroyed by reaction with various partners C,         X + C => D + E (kXC) or by photodestruction,         X + h*nu => products (betaX) is therefore 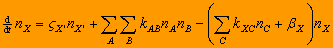        , where X' is a species that, when ionized by cosmic rays at a rate zeta_X', produces the species X, if X is ion. Grain reactions are included in this formula by taking A or B as grains. In this case a loss term should be considered by taking one of C species as the grains. Each of the Ns considered species in the chemistry system has one such equation, so we have a non-linear equation set. There are another two conservatioin equations: conservation of the number density n_M^0 of each elements M,         n_M^0 = SUM_i n_i * c_i^M where c_i^M is the number of atoms of element M in one molecule species i. Another one is the conservation of charge,         ne = SUM_j n_j * c_j^e where ne is the number density of electrons, and c_j^e is the charge (positive or negative) associated with species j. The existance of the two sets of conservation equations indicates that the Ns rate equations are not completely independent to each other. The last constraint to the solution of the chemistry problem is         n_X > 0  for all X. To solve the chemistry problem, we need to specify: cloud geometry, gas density, kinetic temperature, total abundances of each element, cosmic ray field and radiation field. Except for the cosmic ray field, the other factors can all be function of position in the clouds. Dust scattering could be an important factor in determing the radiation field inside the cloud, but in practice, people usually accept the simple but crude approximation of I ~ exp(-tau). For equilibrium, a set of non-linear equation need to be solved. Usually Newton-Raphson technique is used. For time dependent problem, because the evolution equations are stiff equations, specially methods such as implicit Eular method or Trapezoidal method should be used to overcome the difficulties in convergence and stability. Actually chemistry modelers usually use a technique written by C. W. Gear and considerably developed by Hindmarsh to solve the time dependent chemistry.

	Interstellar shocks From the theory of shocks, for a plane shock wave propogating in a uniform gas with density rho0 and pressure P0 (no magnetic field), the post-shock density rho1, pressure P1, velocity V1 and temperature T1 are:         rho1/rho0 = 4; P1 = 3/4 rho0 Vs^2; V1 = 3/4 Vs; T1 = 3 mu Vs^2/16k, where mu is the mean mass per particle immediately behind the shock front and Vs is the plane shock velocity. The temperature also can be written as         T1 = 2900 (Vs / 10 km/s)^2 K  for neutral atomic gas, or          T1 = 1400 (Vs / 10 km/s)^2 K for ionized gas. A fast enough shock ionizes gas and the subsequent H+ recombination radiation may delay or inhibit further recombination or molecule formation. However, when strong magnetic field exists, the jump across the shock front may not be so high and the temperature will be much lower than given by above formulas too. However, T1 can still be > 10^3 K and some chemical reaction will be initiated. Very strong shocks totally ionize all gases, which is not interesting in chemistry. Only shocks with Vs<50km/s is the most interesting for chemistry because gas mostly remains neutral and chemistry can be active.
	The chemical effects of a non-magnetic shock The most important effect of a low/moderate velocity shock is to raise the temperature from typically <100K to ~3000K, so that many slightly endothermic reaction (~0.1-1.0 eV) that were impossible in a typical interstellar cloud will be fast. The high temperature is transient only, because molecular line emission is very strong in high temperature and cools the gas fast. The major coolant in the postshock region is H2 ro-vibrational emission due to its high abundance. The density rises up as a result. If the new chemical products can not be maintained against photodissociation, the cooling effects will be removed.
	Dissociative and non-dissociative shocks For slower shocks that are not ionizing, there are two kinds: dissociative and non-dissociative shocks. In dissociative shocks, most H2 molecules are dissoicated through collisions:          H2 + M = H2* + M          H2* + M = 2H + M or H2* = H2 + h*nu. The shock velocity for the H2 dissociation is typically V_SD = 20 km/s for non-magnetic shocks and V_SD = 45 km/s for magnetic shocks. Because dipole transitions of H2 are forbiden, the radiative relaxation rate through quadrupole radiation is small: ~ 10^-6 s^-1. Therefore, H2 is much easier to dissociate than the other molecules whose radiative relaxation rates are usually large (100~1000 s^-1). At interstellar densities, mainly H2 is dissociated while the other species are not. However, the resulted H atoms will attack all other neutral molecules and reduce them back to contintuent atoms. Only after H2 molecules are formed on grain surfaces and recover its abundance to above 20%, the other molecules can be quickly re-formed. At this moment, the ion-molecule reactions driven by H2 and H3+ can take place as well. Non-dissociation shocks only raise the temperature and densityof the gas, so that more reactions (with slightly higher energy barrier) will be active. The chemistry will be modified a little by this.
	Procedures for modelling shock chemistry First, determine the nature of the shock: ionizing shocks, or dissociating shocks, or non-dissociating shocks. Second, select reactions from database for considered molecules and for given shock velocity Vs. Then, consider cooling function:         L = L1*n1 + L2*n2 + L3*n3 + ... where L is the energy loss per unit volume per unit time, n1, n2, n3, ... are densites of molecules, Li is the cooling rate per molecule i. All molecules can be potential coolants, but in practice the major contributors  are H2, CO, 13CO, HD, H2O and OH. Their Li values are known. H-atom clouds and the CH+ problem The molecule CH+ observed in interstellar medium can not be produced in equilibrium chemistry with high enough density by         C+ + H = CH+ + h*nu         (R = 1.7x10^-17 cm^3s^-1) or          C+ + H2 = CH+ + H        (R = 7.5x10^-15 T^5/4 exp(-4700/T) cm^3s^-1) while the reactions to destroy it are fast:         CH+ + e = C + H         (R = 10^-7 cm^3s^-1 at T = 300 K)         CH+ + H2 = CH2+ + H        (R = 10^-9 cm^3s^-1). Only in the post-shock region where the temperature is high (~3000K), the production of CH+ will be efficient. Then, CH+ is a sensitive tracer of shocks in diffuse clouds. Studies of M. Elitzur and W. D. Watson concluded that shock velocities ~10 km/s in diffuse clouds with low density n(H)<100 cm^-3 and low H2 abundance [H2/H]<~0.1 can produce observed amount of CH+. Calculations showed that in typical diffuse clouds, the high temperature chemistry stimulated by non-dissociative shocks can produce observable abundance of some species such as CO, HCN and N2. If the dust grains can shield some interstellar UV field, more species can exist for a longer time, mainly, CO, CH4, H2CO, CO2, C2H2, CN, HCN, NH3, CS and H2CS. In dark clouds, because of the paucity of ions, non-dissociative shocks mainly enhance neutral molecular reactions that happen with almost every collision. Calculations show that CO is unaffected, H2O is enhanced, particularly S and Si bearing species are enhanced. The SiO is mainly formed by         Si + OH = SiO + H. Sulfur network is inhibited in interstellar clouds at low temperature because in diffuse clouds the reaction         S+ + H2 = HS+ + H and in dark clouds the reaction         S + H2 = HS + H are both endothermic. At high temperature in the post-shock region, these reactions can be active. Then, other molecules such as H2S can form by         SH + H2 = H2S + H and SO can form from         SH + O = SO + H or     OH + S = SO + H         O2 + S = SO + O. SO2 can be formed by the high temperature reaction         SO + O2 = SO2 + O  or temperature independent reaction         SO + OH = SO2 + H.
	Interstellar isotopes Origins of some heavy element isotopes: H burning in MS stars: 13C, 14N He burning in RG stars: 12C, 16O, 18O Novae, SNe, supermassive stars: H zone: 13C, 15N, 17O He zone: 15N, 18O Low mass stars: 13C, 14N Outer region of cool stars: 13C, 14N, 17O (from Hasegawa-san's hand written notes) Little nuclear burning has occured in the Sun. Therefore, the solar isotopic ratios represent interstellar values. Difference from these values indicates production of isotopes from star. The difference in mass of different isotopes can lead to differences in chemistry, hence, sometimes the isotopic molecular abundance ratio doesn't equal to the elemental isotopic ratio, which is called chemical fractionation. Deuterium in diffuse clouds Interstellar D/H = 1.8x10^-5, but observed HD/H2 = ~10^-6 in diffuse clouds. Observations of different astronomical sources also found values widely spreaded around this value. The cause is mainly difference in the selfshielding of interstellar radiation by HD and H2. Because the abundance of HD is much lower than H2, HD almost has not selfshielding and so will be more easily destroyed. Grain formation of HD in diffuse cloud conditions (n=100 cm^-3, photodissociation rate beta(HD) = 10^-10 s^-1) gives n(HD)/n = ~ 10^-8, which is not high enough to account for observed abundances. Ion-molecule reactions         H+ + D <=> H + D+       (left right balanced)         D+ + H2 <=> HD + H+ + dE have two orders of magnitude higher formation rate of HD than grain surface reactions. The second reaction is exothermic because the zero point energy of a harmonic oscillator with force constant C is 1/2*hbar*sqrt(C/mu), where mu is the reduced mass. Deuterium in dark clouds In dark clouds, the above exothermic reaction (D+ + H2) allows D to easily replace H in H2. Therefore, [HD/H2] in dark clouds is higher than D/H ratio. D containing species among some molecules such as HCN, HNC, NH3, HCO+ and N2H+ can be enhanced by a factor of 10^2-10^5. In dense clouds, most D is in HD. Therefore the reaction         XH+ + HD <=> XD+ + H2 + dE can be exothermic for some species X and cause deuterium fractionation. This reaction is important only when XH+ doesn't further react with H2, otherwise, the reaction with H2 dominate the above reaction.  One example is the replacement of H by D in H3+:         H3+ + HD <=> H2D+ H2 +dE with reaction rate of 1.3x10^-9 cm^3s^-1 at T=80K and theoretically dE = 140 K. In dark clouds, H3+ gives rise to HCO+ and N2H+ via         H3+ + CO = HCO+ + H2         H3+ + N2 = N2H+ + H2 and so similarly H2D+ gives rise to deuterated products via         H2D+ + CO = DCO+ + H2   or   HCO+ + HD         H2D+ + N2 = N2D+ + H2   or   N2H+ + HD. If both H3+ and H2D+ are mainly destroyed by dissociative recombination:         H3+ + e = H2 + H   or   3H         H2D+ + e = HD + H   or   D + 2H, then an equilibrium n(H2D+)/n(H3+) ratio can be calculated from the above reactions when n(H2), n(HD), n(CO), n(N2), n(e) and temperature T are known. A rough estimate of this ratio in typical dark cloud is ~0.4, much larger than cosmic D/H = 1.8x10^-5, representing a strong fractionation of D. The example of DCN:         H2D+ + HCN = HDCN+ + H2         HDCN+ + e = DCN + H   or   HCN + D or with the help of         DCO+ + HCN = HDCN+ + CO Another example:         CH3+ + H2 = CH5+ + h*nu Deuterated CH5+ can give rise to fractionation to many other species. Carbon isotope fractionation The concentration of 13C in CO can be achieved via         13C+ + CO <=> C+ + 13CO + dE where the forward rate coefficient is 6.8x10^-10 cm^3s^-1 at a kinetic temperature of 80 K and the zero-point energy difference is dE/k = 35K. Therefore, if the abundances of CO and 13CO are governed by this reaction only, the equilibrium abundance ratio will be          [CO/13CO] = [C+/13C+] * exp(-dE/kT). Hence 13CO will be highly over abundant when T<35K. However, in accual clouds, there will be other reactions involving C+, CO and C.  In the center of dark clouds where interstellar radiation is excluded, all C atoms are in CO and therefore, no fractionation can be expected. But on the edge of the clouds where CO is destroyed by photon and recycled as C+, if the temerature is low enough, 13C fractionation can appear. A side effect of high degree of 13C fractionation in CO is the depletion of 13C in other C-bearing molecules whose formation is linked to gas phase C or C+ in the same region of clouds. The isotopic abundances in HCO+ can in principle be affected by reaction         HCO+ + 13CO <=> H13CO+ + CO + dE with a fast rate coefficient of 4.2x10^-10 cm^3s^-1 at T = 80K and dE/k = 12+-5K. However, in the interior of dark clouds, the reaction pair         CO + H3+ = HCO+ + H2         HCO+ + e = CO + H ensure the close relationship between CO and HCO+. Fractionation of other isotopes Fractionation of 18O in HCO+ can occur in the low temperature dark clouds via         HCO+ + C18O <=> HC18O+ + CO + dE with rate coefficient of 4.2x10^-10 cm^3s^-1 at a kinetic temperature of 80K and dE/k = 15+-5 K. A similar fractionation of 15N in N2H+  can happen via         N2H+ + N15N <=> N15NH+ + N2 + dE with rate coefficient of 4.6x10^-10 cm^3s^-1 at a kinetic temperature of 80K and dE/k = 9+-3 K. Although neutral exchange reactions sometimes can serve as fractionation mechanisms, but they usually encounter substantial activation energy barrier and so become very slow at low temperatures. E.g., the reaction        18O + CO <=> O + C18O + dE with dE/k = 37 K is actually slow at room temperature due to high enery barrier.
	Molecular formation in stellar atmosphere Molecular lines have been observed in stars with cool atmosphere (T<6000K). The molecular abundances are mainly calculated by assuming temperature and density structure of the stellar atmosphere and C/O ratio. The major chemical processes are two-body and three-body reactions, because of the high density (10^11-10^15 cm^-3) and temperature (>10^3K). E.g.:         A + H = AH*         AH* + M = AH + M  For stars with mass loss, the chemistry in the stellar wind is assumed to be frozen in and so keep the identical as equilibrium compsition, because the ejection of matter is fast and there is not much chemical reactions happen during the pass of the atmosphere. In LTE conditions, the equilibrium position for a reaction such as         2H + O = H2O can be determined from the quillibrium constant Kp(H2O) via         Kp(H2O) = p(H2O)/p(H)^2/p(O) = exp(-dG0(H2O)/RT) where p(H2O) etc. are partial pressures, R is the gas constant, and          dG0(H2O) = dGf(H2O) - 2dGf(H) - dGf(O) with dGf(X) being the standard free energy of formation of X. The partial pressure p(X) is related to the number density n(X) through p(X) = n(X)RT. The standard free energies for many compounds of interest in a stellar atmosphere are available. Combining the above quillibrium constant equation for all interesting conpound with the particle conservation relation of all involved elements, one can calculate the equilibrium chemical composition for a given atmosphere condition. Grains can form when the partial pressure of an element or compound exceeds the vapour pressure. Alternatively, a specific supersaturation can be required before grain are formed. 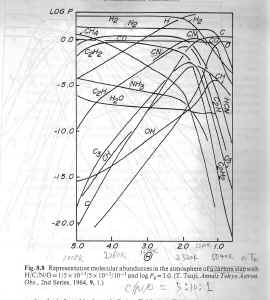As shown in figures below, calculations showed that in C-rich stars: almost all O is combined in CO; most C is contain in CO and C2H2; N is primarily found as HCN and N2; S is mainly contained in SiS, CS and H2S; Si is in the form of SiO, SiC2 and Si2C. In O-rich stars: OH and H2O have comparable abundance as CO, C is (?), N is in N2, S is in (?), Si is mainly in SiO and dust grains. (figures: left -- LET chemistry results in O-rich stars; middle -- in C-rich stars; right -- in C-rich stars with dust grains.) In carbon stars, when dust grains form, the abundance of C2H2 and CH4 will reduce much due to the shortage of C.
	Molecules in circumstellar shells Neither of the two important molecular ions in ion-molecule chemistry: HCO+ and N2H+ are detected in IRC +10216, and the observed HCN/HNC = 100 in this star is also much larger than interstellar value of ~ 1. Therefore, typical interstellar chemistry may don't occur in the CSE, LTE chemistry could be frozen out. Characteristic expansion time constant can be estimated as          tau_exp = n/Ve/(dn/dr) where n is gas density, Ve is the expansion velocity. For steady stellar wind with n~r^-2, this becomes         tau_exp = r/2Ve. For a neutral reaction         A + B = C + D with rate coefficient k = A exp(-dE/kT), the condition for frozen out of A is         k * n(B) * tau_exp > 1.   (for steady wind model: ~ r^-1*e^-r) Different species have different energy barrier dE and so have different 'freezing out' radii. Some reaction involving little activation barrier, such as radical-radical combinations, will occur further out into the CSE. In the outer part of the CSE where dust shielding is weaker, photodissociation of some species will initiate more photo-chain reactions.

	Many hundreds of reactions have been included, but many reaction rates are guesses. More laboratory measurements are called for.
	The nature of interstellar grain is largely unknown. More infrared observations are needed.
	Observational errors, uncertain oscillator strength, unknown Doppler parameters in a curve of growth analysis prevented proper choice of chemical models.
	Still need to consider geometric effects, grain albedo and phase function parameters, density and temperature structures of clouds, uniqueness of solution.
	Need to consider more issues: chemistry-cooling-cloud evolution; chemistry-grain disruption; formation of some intriguing species such as polyynes; pathological cases such as the presence of HCS+ and CO+.