Special topics related to binaries

Binary

Caution!! Although I am happy to share my research notes below with all visitors to my webpages, these pages are mainly designed for my own use and subject to change without warning. I do not guarantee the correctness of all contents as well.

Special topics related to binaries (definition in Wiki entry)

	Catalogues of binary
	Textbook of binary
	Stellar types related to binary
	Observations of binary
	Theory and modeling of bianry

Catalogues of binaries: (back to top)

	9th Catalogue of orbit elements of spectroscopic binaries (SB): here. More late-type systems than in SB8. Statistics show two peaks of period of SB1 around 4 days and 1200 days, while two peaks of period of SB2 around 0.4 day and 4 days. The lack of peak of SB1 at 0.4 day is difficult to explain, while the lack of peak of SB2 at 1200 days could be due to blending of spectral lines (I think it could be due to the much lower velocity of the heavy primary in the large orbit.) The upper envelope of the e-P distribution is better fit by P(e-1)^3 = const., instead of the expected fixed periastron distance a(1-e) ~ P^2/3(1-3) = const. (from Pourbaix et al., 2004A&A...424..727P)
	CHARA Catalog of Orbital Elements of SB. Predicted angular separation of components are given. (from Taylor et al., 2003PASP..115..609T)
	8th Catalogue of orbit elements of spectroscopic binaries (SB): here.
	18 binaries orbits with red giant components are listed on page 95 of the book by Peter Eggleton (2006epbm.book.....E). 9 of them are not listed in the 8th catalogue of orbit elements
	29 non-catalysmic binaries involving Hipparcos M giants. (from Famaey et al., arXiv.0901.0934) (back to top)

Some notes on binaries from the book 'Evolutionary Processes in Binary and Multiple Stars' by Peter Eggleton (2006epbm.book.....E).

Spectrum analysis of a single star only yields parameters such as surface temperature, gravity and composition, while the mass or radius can be constraint only by observation of a binary (except the case of white dwarf that has a tight radius-mass relation and thus both can be inferred from gravity).

Determine orbital parameters with different data:

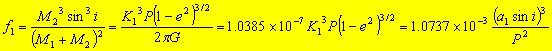
	Single line spectroscopic binary (SB1): P, e, radial velocity amplitude K or projected major axis asini~KPsqrt(1-e^2). Then the mass is related to the mass function: where M₁ is the mass of the observed star and M₂ is the mass of the unseen star. Units are: K₁ in km/s, P in days, a₁sini in light-seconds and masses in solar mass. The inclination angle i usually can not be measured. If we adopt an average value of 1/sin³i = 1.25. Then with the definition of mass ratio q = M₁/M₂, we have M₁ ~ 1.25 q (1+q)² * f₁ M₂ ~ 1.25 q * (1+q)² * f₁
	Double line spectroscopic binary (SB2): in addition to P, e, and K, the mass ratio q can be obtained. But i is still unknown.
	Visible double line spectroscopic binary (VSB2): in addition to P, e, K and q, both M1, M2, i and distance D can be determined in favorable cases. Here D is independent of parallax.
	Photometric binary or eclipsing binary (EB): P, e, i, the ratio R1/a, R2/a of stellar radii to orbital semimajor axis, and the temperature T2 (provided that the temperatue of the brighter star T1 is known from spectroscopic analysis).
	Eclipsing double line spectroscopic binary (ESB2): all parameters P, e, i, a, M1, M2, R1, R2, T1, T2 and D can be determined. One of the two temperature should be determined from stellar atmosphere modeling of spectrum. However, for extreme cases, such as O, M stars, supergiants or subdwarfs as component of the binary, some other factors such as mass loss, instability, convection and metallicity might prevent the parameter determination.
	Distorsion of the component stars, one-side warm-up of the cooler component by the illumination of the hotter one (reflection effect), gas streams and starspots induced by mass exchange, etc. can cause unusual features in the light curve. Apsidal motion (caused by deviation of the force from inverse square law due to general relativity effects and non-sphericity of the star) and third body can periodically affect the minima of the light curve (seen in the O-C diagrams).

Multiple systems with more than 2 components tend to be hierarchical. E.g., one close binary with a distant third body. The stable range of orbit size ratio is however highly dependent upon eccentricities and inclinations between the outer and inner orbits. See Evans (1968QJRAS...9..388E and 1977RMxAA...3...13E).

In triple system, when the outer orbit is highly inclined w.r.t. the inner orbit (i> 39deg), Kozai cycles will occur, say, the eccentricity of the inner orbit fluctuates cyclically bwtween a small and a large value on a timescalse of (P_outer^2/P_inner) * (M_total/M_3rd). See Kozai (1962AJ.....67..591K)

IMF of binary is roughly the same as that of single star: N ~ M^-2.35 when M>0.01 Msun and N = 0 when M < 0.01 Msun. (see Salpeter, 1955ApJ...121..161S).

Currently known period distributions: N ~ P^-0.7 for P< 30yrs; N~p^-1.3 for P > 300 yrs. But it is strongly affected by the detectability of binaries with different periods. Periods between 0.1~10^4 years are difficult to detect.

The distribution of mass ratio and eccentricities are more uncertain. Eccentricities seem to be equally distributed between 0 and 1.

Single star evolution:

Formmulas for single star evolution on MS (with solar metallicity: X=0.7, Y=0.28, Z=0.02 and L, M, R in solar units):

	Luminosity: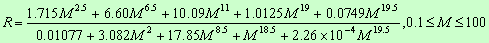
	Luminosity in V band (~0.5-0.6um):
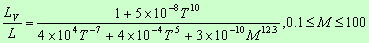
	Luminosity in B band (~0.4-0.5um):
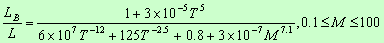
	Stellar radius:
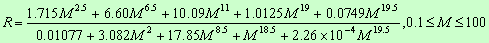	Stellar surface temperature in kK: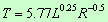
	Life time on the main sequence band in Myrs: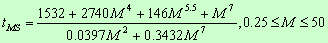

Computed models of MS stars show the stellar structures:

	Stars with M<0.3Msun: wholly convective;
	Stars with 0.3Msun<M<1.1Msun: radiative core and convective envelope;
	Stars with 1.1Msun<M<1.25Msun: core starts with radiative equillibrium and developes convections across the MS band;
	Stars with M >1.25Msun: convective core and radiative envelope.

Initial-final mass relation: Mf = max [ 0.51+0.049*Mi, min ( 0.35+0.11Mi, 0.60+0.06Mi)] for 0.8 < Mi < 7.5 (see Han et al., 1994MNRAS.270..121H) or Mf ~ 0.4 +0.05Mi + 0.00015Mi^4 for 1 < Mi < 8. (see Weidemann & Koester, 1983A&A...121...77W).

Because the lifetime during the red giant phase is much shorter than on the main sequence, the ZAMS component usually does not evolve much during the red giant phase its companion. Thus there are two typical cases of a red giant binaries: (1) the hotter companion is a white dwarf that has a higher initial mass and has evolved over the red giant phase (its ZAMS mass is higher); (2) the hotter companion is a ZAMS star with lower initial mass. There could be a much rarer intermediate case in which both companions are red giants.

Mass loss rate law of red giants: (1) Mlr ~ -10^-6.4 eta*L*R/M (all in solar units and megayear) from Reimers (1975MSRSL...8..369R), with eta a fudge factor arbitrarily chosen to reach reasonable final core mass; (2) Mlr ~ -10^-7.6 (R^2/M)^1.43 from Judge & Stencel (1991ApJ...371..357J), which can be curiously extrapolate to the Sun. The mass loss rate law of luminous hot stars was given in Chebyshev polynomials by de Jager et al., 1988A&AS...72..259D. Nine types of mass loss can be listed:

a fast, hot, meagre, Solar-like wind in cool (GKM) dwarfs and in some GK giants
a slow, cool, meagre wind in M giants and some GK giants
a slow, cool, copious wind (superwind) in late M giants (AGB) stars
a very fast, hot, meagre wind in PN neuclei (post-AGB, pre-WD)
an episodic, meagre, rotating wind in Be stars
a fast, meagre wind in Of stars
a fast, copious, episodic wind in LVBs (P Cyg)
a very fast, somewhat less copious wind in WRs
an almost instantaneous, copious wind in a supernova explosion

Unresolved problems:

mixing length treatment lacks of theoretical support
overshooting treatment
semiconductive mixing not included
diffusive separation of elements not included
model for mass loss
model of rotation and its consequence to stellar evolution unknown
model for dynamo activity
model for photospheres with wind effects

Binary evolution modes and cases:

3 modes of evolution according to RLOF timescales:

	mode 1 -- nucelar;
	mode 2 -- thermal;
	mode 3 -- hydrodynamical

4 cases of evolution with RLOF:

	case A -- the loser is still in the main sequence band;
	case B -- the loser is in the Hertzprung gap and therefore has a mainly radiative envelope;
	case C -- the loser is in the giant branch and therefore has a mainly convective envelope;
	case D -- wide binary system without RLOF (list for completeness).

Effects of interaction process to the binary orbit:

------------- slow non-conservative processes --------------------

GR -- gravitational radiation: tends to circularise the orbit and reduce the period and orbit size on a long timescale.

TF -- tidal friction: tends to circularise the orbit and produce corotation of both stars with the orbit.

RLOF -- Roche lobe overflow: first decreases P and then increase it when the mass ratio pass through unity.

Wind processes: increases P and orbit size, but spin down the losing star. (including NW -- normal single-star wind; MB -- magnetic braking with tidal friction; EW -- binary-enhanced stellar wind; PA -- partial accretion of stellar wind; BP -- bipolar re-emission)

MB -- magnetic braking: if the orbit shrinks or expands depends on the ratio of alfven radius to orbital radius.

EW-- binary-enhanced stellar wind: single-star spin-down timescale of stellar wind is about 1/10 of the mass loss timescale.

TB -- third body: causes precession, apsidal motion and eccetricity variation of the inner orbit. The effect is more prominent for smaller outer orbit or larger inclination of the outer orbit. Particularly, when the inclination angle is >39deg (=1/sins[qrt(2/5)]), the Kozai cycles can be surprisingly large even when the outer orbit is quite wide. Some other perturbations such as rotation, mutual distortion and gravitational wave can produce variation of e as well, but they drop off rapidly with the inner orbit size. Thus, for a given inner orbit size, there is a maximum outer orbit size within whitch Kozai cycle is significant, but this upper limit is still several thousand times larger than the inner orbit. In a long run, the Kozai cycle can couple with tidal friction near periastron when e is the largest to continously remove energy and angular momentum from the orbit motion. In this case, the inner orbit shrinks, while the outer orbit expands.

Several examples of triple systems are given on page 207. Only one owns an M III giant and a catalysmic binary: CQ Dra -- [(WD+?; SD, 0.16days) + M3III; 4.7years, e=0.3, f = 0.0076 Msun], see Reimers et al., 1988A&A...193..180R.

------------- rapid non-conservative processes --------------------

DI -- Darwin instability: in the case where two stars with large mass ratio q are corotating due to tidal friction coupling, the stellar radius of the bigger component has a maximum value beyond which the star will begin to take angular momentum from the orbit motion (I still don't understand why!!). Subsequently, the orbit will shrink and become more eccentric. Then, the very small secondary will very possibly plung into the envelope of the bigger star near the periastron and thus develope a common envelop (CE). The secondary will either be smeared out in the CE or blow away the CE (if the orbit motion is energetic enough).

CE,EJ -- Common envelope, ejection (hydrodynamical mass transfer): when the two companions get close enough, particularly in an eccentric orbit, the secondary will be engulfed into the envelope of the primary to form common envelop (CE), such that a large fraction of angular momentum and energy can be transfered to the gas in the CE. As a result, the secondary is braked and gradually spirals in towards the core of the primary and thus the mutual orbit will shrink. There are two possible end products: (1) enough energy and angular momentum are transferred to the gas and eject the CE, with a more compact binary left; (2) the secondary is smeared out and merged with the primary core--merger.

SN -- Supernova explosion: if the SN explosion is instantaneous and isotropic, the separation and velocities do not change after the SN explosion. In this case, if the mass of the residual neutron star or black hole is less than 1/2 of the original mass, the binary will become unbound. If the SN explosion is anisotropic, the kick effect can either disrupt the binary system or push the resulted neutron star or black hole towards its companion.

DE -- Dynamical encounter: This occurs mainly in clusters. More massive stars like neutron stars and close binaries tend to sink into the center of the cluster and interact there.

Accretion by the companion

	Four zones from inside to outside around the accretor: (1) a magnetospheric zone in which a magnetic field anchored in the rotating gainer dominates the flow and matter is accreted onto the star along the magnetic lines; (2) a Keplerian disk region in which centrifugal force largely balances gravity in the radial direction, while viscocity drives an inward gas flow and an outward angular momentum flux; (3) an inward free-fall region where the specific angular momentum of gas is small compared to the Keplerian specific angular momentum; (4) a wind region around the loser.
	The viscocity in the accretion disk is the most probably from magnetic field and turbulence, although the source turbulence is still unclear.
	Possible energy source of jets: (1) magnetic pressure; (2) coronal heating above the disc; (3) nova-like thermonuclear burning on the WD surface (but not the neutron star surface, because the gravity is too strong to allow outflow).

Stellar types related to binary, roughly along the evolutionary sequence: (back to top)

	Normal optical bianry:
	Algol star: semi-detached bianry in which the larger, more evolved stars has lower mass than its companion.
	Abell-35 subclass of PNe:
	Ba dwarfs (including the so-called WIRRing stars)
	CH star: G5-K5 giants with very strong CH bands and enhanced heavy elements such as Sr and Ba.
	Barium star: G2-K4 giants showing very strong Ba II lambda 4554 line.
	Extrinsic (Tc-poor) S stars or C stars
	Catalysmic variable (CV): semi-detached bianry system consisting of a WD and MS star in which mass transfer is stable on a long time-scale.
	d'-type yellow symbiotics:
	[?]Symbiotic star: stars with outstanding spectrum in which there are emission lines as PNe, while the continuum indicates a relatively low temperature and absorption lines correspond to spectral type M and luminosity type II-III. The secondary is either an MS star (in Algol-like symbiotics) or a WD (in nova-like symbiotics). They could be the early (MS) and late (WD) stages of the Ba star evolution.
	[?]Red s-type symbiotic stars, not s-processes enrichment.
	post-AGB binaries (with or without enrichment of s-processes)
	Double degenerate stars (DDs): binaries consisting of two degenerate stars.

Other observations: (back to top)

	Substantially more than 50% of stars are short-period binaries. (from Petrie, 1960AnAp...23..744P)
	Nearly 100% stars are in binaries. (from Poveda et al., 1982ApJ...258..589P)
	Normal and abnormal bianry frequencies of main sequence stars are reviewed. The correlation between high/low duplicity and consequent peculiarities are produced by different dynamical and astrophysical mechanisms. (from Abt, 1983ARA&A..21..343A)
	Goldin, Alexey; Makarov, Valery 2007arXiv0706.0361G found old disk wide binary HIP 754, the nearby AGB star HIP 34922 (L2 Pup), and the nearby M2 dwarf HIP 5496 (GJ 54, at 8 pc from the Sun) which has a resolved M dwarf companion.
	With their radial velocity data of a selected sample of Hipparcos sources, they identified 12 new binaries with M giant component, and thus raised the total number of such evolved binary systems to 29. However, M giants involving Mira variables have been excluded from their sample because the confusing radial velocity jitter presented in Mira and SR variables. (from Famaey et al., arXiv:0901.0934)
	They find that the detection rate of binary among field M giants is 6.3%-11.1%, larger with more monitoring data points, but less than that of K giants. Intrinsic line width Sb (with instrumental width removed) of all binaries is correlated best with stellar radius R, instead of previously thought luminosity or effective temperature. Two outliers of Sb-R relation (HD 190658 and HD 219654) turn out to be binary-induced fast rotators. M giant binaries have Sb < 5 km/s, perhaps because of the larger size of M giants. (from Frankowski et al., 2009arXiv0901.0937F)
	They use a new set of orbits to construct the first e-logP diagram of M giant binaries. They found that the orbital elements are not very different among binaries with M giants, post-AGB stars, Ba stars and Tc-poor S stars, indicating that (1) post-AGB stars in binary left AGB at an early stage (M4 or so); (2) binary systems with e<0.4logP-1 are predominantly post-mass-transfer systems (with WD companion of 0.6Msun, like the Ba stars and the Tc-poor S stars); (3) they also found lack of M giant biaries with period<80days and period(>800days but with small e. There is almost no M giant binary with circular orbit! (from Jorissen et al., arXiv:0901.0938) (fig: evolutionary sequence of different peculiar types of objects, with hatched circles standing for C and heavy metal enhanced stars. The left numerated column represents single star evolution sequence while the right graphic column represents binary evolution sequence. Some annotations are added by I.)
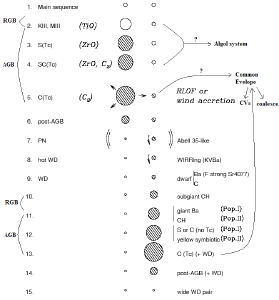	They identified 19 new close bianry CSPN (central star of PN) in the Galactic bulge via the OGLE microlensing survey and thus more than doubled the total number of CSPN to 21. The derived an independent estimate of close binary fraction of 12-21% among the sample of PNe, confirming previous estimate of 10-15% and suggesting that binarity is not a precondition for the formation of PN. Most of the orbital periods P are shorter than 1 day. The period statistics is best reproduced by CE population synthesis models when no correlation between primary and secondary masses is assumed for the initial mass ratio distribution. (from Miszalski et al., arXiv:0901.4419)

Theory and modeling of binary: (back to top)

They discussed the four possible channels of the formation of Ba/CH stars: (1) wind accretion (stellar wind + superwind); (2) wind exposure (all envelope mass lost due to binary enhanced wind before the onset of superwind); (3) stable RLOF (stellar wind + RLOF); (4) common envelope ejection (stellar wind + CE ejection). Their models can well explain observed Ba star number, orbital period and mass function distributions of Ba and CH stars. They found that strong Ba stars are formed through channels (1,2,3) while mild Ba stars are formed through channels (1,2). The average mass of strong Ba and CH stars are 1.8 and 1.2 Msun respectively. The average mass of WD in the Ba and CH binaries are 0.6 and 0.62 Msun respectively. They also found that the maximum stellar mass for s-processing is 2 Msun. (from Han et al., 1995MNRAS.277.1443H)

They re-examined the prograde and retrograde three-body hierarchical systems and studied the dependence of stability region upon its parameters. (from Donnison & Mikulskis, 1995MNRAS.272....1D)

Accretion of circumstellar matter can produce jets and bipolar structures: Soker 2002, ApJ, 568, 726 and Frank, A. & Blackman, E. G. 2004, ApJ, 614, 737.

They attempted to make a unified theory for after-AGB binary evolution. It involves following types of binary systems:

	Ba stars: G-K type giants with overabundance of Ba
	Abell-35 subclass of PNe
	Ba dwarfs (including the so-called WIRRing stars)
	subgiant/giant CH stars
	extrinsic S stars
	d'-type yellow symbiotics
	post-AGB binaries (with or without enrichment of s-processes)
	Red s-type symbiotic stars with a massive WD companion (> 0.5 Msun), not s-processes enrichment.
	catalysmic variables (CVs) with massive WD companion (> 0.5 Msun).

They posed an evolutionary 4-step trancient torus scenario for post-AGB binaries step by step: (1) wind accretion that lose angular momentum; (2) evolutionary expansioin of the red giant cause Roche lobe overflow through L1 point; (3) leak of matter through L2 point forms ejecta that eventually fall back to collide with the latter ejected winds to form a rotating torus; (4) while most matter is eventually pushed away by radiation presure on dust, a small amount of matter retains to form circumbinary Keplerian disk. (from Frankowski & Jorissen, 2007BaltA..16..104F)
(fig: a 2D scheme of the different types of after-AGB binaries.)

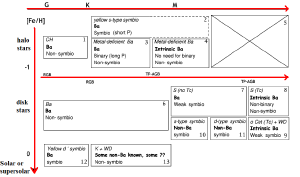The Bondi-Hoyle-Lyttleton accretion was reviewed together with later numerical studies. When a point source moves through a uniform medium, the amount of matter accreted by the point source is:

Hoyle-Lyttleton accretion with pressure free gas:

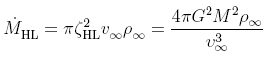
where v_inf and rho_inf are the velocity of the point source and the density of the gas, zeta_HL is the so called Hoyle-Lyttleton radius of a column within which the gas is assumed to be all accreted because it is bound, M is the mass of the point source.

Bondi-Hoyle accretion with gas pressure considered:

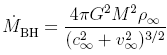
where c_inf is the sound speed in the gas.

(from Edgar, 2004NewAR..48..843E)

[ previous ] [ upper ] [ next ] Welcome comments to me: jinhuahe

ynao.ac.cn [back to my Home]