Caution!! Although I am happy to share my research notes below with all visitors to my webpages, these pages are mainly designed for my own use and subject to change without warning. I do not guarantee the correctness of all contents as well.
![]()
|
Caution!! Although I am happy to share my research notes below with all visitors to my webpages, these pages are mainly designed for my own use and subject to change without warning. I do not guarantee the correctness of all contents as well.
|
Bensch et al., 2001, A&A, 365, 285 (all
efficiencies mentioned, very good!!!!) Conversion of votage counts into antenna temperature
(from ARO-HHT document, page 294): First observe a hot load of room temperature (e.g.,
280K), the count is C_hot. R = (280K - 80K) / (C_hot - C_cold). Because counts are usually proportional to input flux (expressed in temperature). The ratio R is expected to be constant for all observations. Therefore, multiplying R to the counts derived towards real source, we get the measured antenna temperature at once. (? Is the counts for zero K really 0 count? If not, we should take the cold or hot load as reference point for converting counts in to Kelvin. Then, we have formula R = (T_source - 80K) / (C_source - C_cold). Therefore, the formula for T_source is T_source = 80K + R * (C_source - C_cold) right?)
Antenna beam Omega_A and diameter D: The effective antenna beam solid angle is Omega_A = lambda^2 / A_e = lambda^2 / A_p / eta_A, where A_e is the effective antenna area, A_p = 0.25*PI*D^2 is the physical antenna area, eta_A is the aperture efficiency.
Gaussian main beam Omega_mb and main beam size theta_b: The main lobe of the antenna beam pattern (power pattern) is called the main beam. The main beam usually can be well approximated by a gaussian function (normalized to a maximum of 1). It is called a gaussian main beam. The gaussian beam is frequently used in formula deduction for single dish. The size of a gaussian beam is characterized by FWHM of the power pattern: theta_b. Then solid angle of such a gaussian beam is Omega_mb = int{exp[-4ln2 * theta^2/theta_b^2] * 2*PI*theta}d(theta) = PI/4/ln2 * theta_b^2 =~ 1.133 * theta_b^2. The last equation has accuracy of about 5%. An accuracy of 1% can be obtained by using the 0.1 power beam size theta_0.1: Omega_mb = int{exp[-4ln10 * theta^2/theta_0.1^2] * 2*PI*theta}d(theta) = PI/4/ln10 * theta_0.1^2 =~ 0.3411 * theta_0.1^2. (from K. Rohlfs and T.L. Wilson, 'Tools of Radio Astronomy', third revised and enlarged edition, 1996, Springer, page 190-191.)
Under Reyleigh-Jeans approximation, flux density can be computed from antenna temperature T'_A (corrected for antenna efficiencies eta_r, eta_fss and eta_rss) or main beam temperature T_mb. According to the definition of T'_A, the total amount of received radiation flux is equivalent to what we can get by pointing the same antenna to an infinitly large and homogeneous blackbody with R-J temperature T'_A. Hence, the flux is S_nu = B_nu(T'_A)*Omega_A = (2k*T'_A/lambda^2) * (lambda^2/A_e) = (2k/A_e)T'_A = 3520 * T'_A[K]/eta_A/D^2[m^2] [Jy/K]. In the last equation, D is physical diameter of the antenna aperture. According to the definition of T_mb, the total amount of received radiation flux is equalent to what we will get by point a Gaussian beam with beam solid angle of Omega_mb to an infinitely large and homogeneous blackbody with R-J temperature T_mb. Omega_mb is related to whole antenna beam Omega_A through main beam efficiency eta_mb = Omega_mb/Omega_A. Hence, the flux is S_nu = B_nu(T_mb)*Omega_mb = (2k *T_mb/ lambda^2) * (lambda^2*eta_mb/ A_e) = (2k/A_e)T_mb*eta_mb. Actually the above two sets of formulas can be directly related to each other through eta_mb = T'_A/T_mb. ;) Therefore, once we know the effectvie antenna area (or physical diameter together with aperture efficiency), we can convert antenna temperature in K into flux density in Jy. Note that beam filling factor has no role in this Jy/K conversion factor. Alternatively, if we know the angular diameter of the effective beam (or main beam) phi("), then (from Dr. Tatsuhiko Hasegawa): Snu = 2k/lambda2 * int{ TB(Omega) } d Omega = 2k/lambda2 * Tmb(obs) * Omegamb (definition of mainbeam temperature) = phi2(")/lambda2(cm)*Tmb(obs) * 7.354x10-4 [Jy] (solid angle Omega = 1.133 * FWHM^2 != pi * sigma^2 / 4, and phi = FWHM ) = phi2(")*freq2(GHz)*Tmb(obs) * 8.182x10-7 [Jy] (solid angle Omega = 1.133 * FWHM^2 != pi * sigma^2 / 4, and phi = FWHM) = 4656.864 * Tmb(obs) / D(m)2 [Jy] (used phi = 1.22 * lambda / D, only suitable for rough estimate!!) Inversely, Tmb = Snu * lambda2(cm) / phi2(") * 1.360 X 103 [K] = Snu / freq2(GHz) / phi2(") * 1.222 X 106 [K] = Snu * D(m)2 * 2.147x10-4 [K]
How to measure aperture efficiency eta_A and main beam efficiency eta_mb: (partly from ARO_HHT document, page 295-296) We assume the main beam diameter theta_mb is already known. Then we can observe a planet that is smaller than the antenna main beam size but not too small to determine the two telescope efficiencies. Let's assume angular diameter theta_p and surface blackbody temperature T of the planet is known (from ephemeris prediction, see, e.g., the SMA webtool or the JPL HORIZONS System). The we start from the definition of the two efficiencies: eta_A = A_e / A_p, eta_mb = Omega_mb / Omega_A, where A_e and A_p are the effective and physical area of the antenna aperture while Omega_mb and Omega_A are the main beam and total beam solid angle, respectively. First, we need to determine eta_A by observing the planet. The observed flux density, under Rayleigh-Jeans approximation, is S_obs = 2k * T'_A / A_e, where T'_A is the observed antenna temperature. Assuming the antenna main beam is a gaussian beam, the planet is a homogeneous disk with angular diameter theta_p, then according to gaussian beam-disk coupling formula S_obs = int{ J(T) * Pn(r,phi)}dOmega where Pn(r,phi) is the normalized gaussian beam pattern (the main beam), PI/4/ln2 * theta_mb^2 = Omega_mb. Then we get eta_A = (2k*T'_A / A_p) * (4ln2 * theta_p^2/theta_mb^2) * 1/{pi*theta_p^2*J(T)*[1-exp(-4ln2 * theta_p^2/theta_mb^2)]} Then, with the relationship lambda^2 = A_e * Omega_A, we get eta_mb = (A_p * Omega_mb / lambda^2) * eta_A
How to measure different telescope efficiencies: (from Kutner, Mundy and Howard, 1984ApJ...283..890K)
How to measure antenna beam shape: Total power drift scan mapping of planet such as Jupiter and Venus at different frequencies to characterize the beam shape at these frequencies. (The planets are usually taken as homogeneous disk sources.) N.B.: Each mapping measurements should be performed in a small hour angle range, otherwise, the telescope rotates when tracking the planet and so smear out the true beam shape.
How to measure antenna error pattern: Drift scan mapping of the Sun at a representative frequency to characterize the error pattern shape. N.B.: The mapping measurements should be performed in a small hour angle range, otherwise, the telescope rotates when tracking the planet and so smear out the true beam shape.
Frequency dependence of aperture efficiency: (from Baars J.W.M., 1973, IEEE transactions on Antenna and propergation, AP-21, No. 4, 461; Ruze R., 1966, Proc. IEEE, 54 No. 4, 633) (The formula from the two literature was cited by Kutner, Mundy and Howard, 1984ApJ...283..890K) eta_A / eta_A0 = exp(-16PI^2<eps^2> / lambda^2), in which eta_A0 is the aperture efficiency of a perfect reflector (infinite wavelength limit), <eps^2> is the mean squared reflector deviation due to random surface errors. This is also one of the possible ways to calculate the reflector surface errors, if a serials of eta_A values have been known at different lambda. However, there are actually other factors that affect the aperture efficiency. Here is a more complete description from GMRT webpage (http://www.gmrt.ncra.tifr.res.in/gmrt_hpage/Users/doc/WEBLF/LFRA/node172.html): The aperture efficiency of an antenna was earlier defined to be the ratio of the effective radiating (or collecting) area of an antenna to the physical area of the antenna. The aperture efficiency eta_a of a feed-and-reflector combination can be decomposed into five separate components: (i)?the illumination efficiency or taper efficiency eta_t, (ii)?the spillover efficiency eta_S, (iii)?the phase efficiency eta_p, (iv)?the crosspolar efficiency eta_x and (v)?the surface error efficiency eta_r. eta_A = eta_t * eta_S * eta_p * eta_x * eta_r The illumination efficiency (see also Chapter?3, where it was called simply ``aperture efficiency'') is a measure of the nonuniformity of the field across the aperture caused by the tapered radiation pattern (refer Figure?19.2). Essentially because the illumination is less towards the edges, the effective area being used is less than the geometric area of the reflector. It is given by
where g(r) is the aperture field. Note that this has a maximum value of 1 when the aperture illumination is uniform, i.e. g(r)=1. The illumination efficiency can also be written in terms of the electric field pattern of the feed E(theta), viz.
where theta_0 is angle subtended by the edge of the reflector at the focus (Figure?19.1). When a feed illuminates the reflector, only a proportion of the power from the feed will intercept the reflector, the remainder being the spillover power. This loss of power is quantified by the spillover efficiency, i.e. Note that the illumination efficiency and the spillover efficiency are complementary; as the edge taper increases, the spillover will decrease (and thus eta_S increases), while the illumination or taper efficiency eta_t decreases19.1 The tradeoff between eta_S and eta_t has an optimum solution, as indicated by the product eta_s * eta_t in Figure?19.3. The maximum of eta_s*eta_t occurs for an edge taper of about -11 dB and has a value of about 80 %. In practice, a value of -10 dB edge taper is frequently quoted as being optimum. 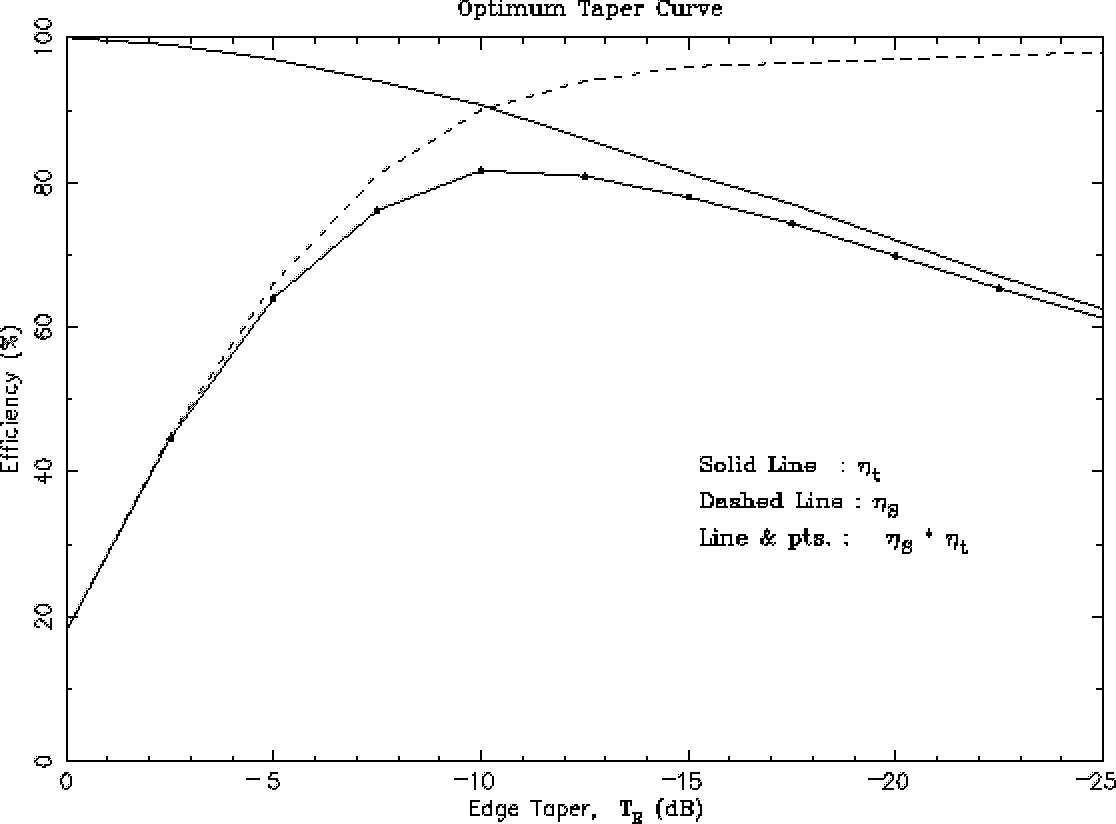
The surface-error efficiency is independent of the feed's illumination. It is associated with far-field cancellations arising from phase errors in the aperture field caused by errors in the reflector's surface. If delta_p is the rms error in the surface of the reflector, the surface-error efficiency is given by (the Ruze formula) eta_r = exp[-(4 * pi * delta_p / lambda)^2] The remaining two efficiencies, the phase efficiency and the cross polarization efficiency, are very close to unity; the former measures the uniformity of the phase across the aperture and the latter measures the amount of power lost in the cross-polar radiation pattern. For symmetric feed patterns[6], eta_x is defined thorough the copolar C_p(theta) and cross-polar patterns X_p(theta):
C_p(theta) = 1/2 [E(theta) + H(theta)] X_p(theta) = 1/2 [E(theta) - H(theta)]
It can be seen that if one can design an antenna, having identical E(theta) & H(theta)
patterns the cross-polar pattern will vanish. Taking the cue from this, the feed for antenna could also designed with a goal to match E and H patterns at least up to the subtended angle of the dish edge,
theta_0.
The purpose
is to determine zenith optical depth tau0. (from ARO 12M online manual, Chapter
6) When an antenna is pointed to a empty
sky area, the antenna temperature is T_A(z) = Trx + T_atm*eta_l*[1-exp(-tau0*A(z))] + T_amb*(1-eta_l)
+ Tbg*eta_l*exp(-tau0*A(z)). Here, Trx is receiver noise temperature, T_atm is Rayleigh Jeans temperature of the
atmosphere, Tamb is ambient Reyleigh Jeans temperature, Tbg is the background
emission from outside of the atmosphere, eta_l is feed efficiency
(=eta_r*eta_rss*eta_fss), tau0 is zenith optical depth, A(z) is air mass at
zenith angle z (A(z)=1/cos(z) for idea weather condition). With vane
calibration, the antenna temperature when the vane is put before the receiver is T_A(vane) = Trx + Tvane. The difference between sky and vane temperatures is dT_A(z) = T_A(vane)-T_A(z) = Tvane - T_atm*eta_l*[1-exp(-tau0*A(z))] - T_amb*(1-eta_l) - Tbg*eta_l*exp(-tau0*A(z)) In practice, we usually roughly assume Tvane = T_atm = T_amb, Tbg = 0 and
eta_l = 1.0, so we have ln(dT_A(z)) = ln(T_amb) - tau0 * A(z) Use the telescope
to observe several empty sky positions with different z, will allow to determine
tau0. This is the so called skydip.
A taumeter is just a smaller telescope specially used to determine tau0 frequently. With the chopper wheel (or vane) method for spectral line calibration, the
effective system temperature that includes corrections for atmospheric attenuation
and antenna spillover, blockage, and ohmic losses but not for error pattern losses
(as the error beam will couple differently to different sources) is T^*_sys = (1+Gi/Gs) * [Trx +
T_A(sky)] / eta_l / eta_fss / exp(-tau0*A). Here Gi and Gs are the gain of the image and signal sidebands, Trx is the
receiver temperature, T_A(sky) is the sky noise (including the signal from
objects), eta_l and eta_fss are telescope efficiencies, tau0 is the zenith
atmospheric opacity, A is airmass. The T_A(sky) is composed of three parts: T_A(sky) = Tsky + Tant +
Tcmbr Here, Tm is the mean atmospheric temperature, Tspill is the spillover
temperature and, Tbg is the cosmic background radiation temperature. Note that
all T's are Rayleigh-Jeans temperatures J(nu,T). Then the
rms noise temperature for beam or position switch observation with half time on
source half time off source is T_rms = 2 * T^*_sys /
eta_spec / sqrt(dnu * t_scan) Here, eta_spec is the spectrometer efficiency (e.g., it is 0.81 for MAC and
1.0 for FB at the ARO 12M telescope), dnu is frequency width in Hz, t_scan is
total exposure time in sec.
(see Wiki entry) It
is a cross-correlation of a signal with itself. The definition for a continum
signal f(t)
is Wiener-khinchin
theorem states that the power spectral density of a wide-sense-stationary
random process is the Fourier transform of
the corresponding autocorrelation
function. That is to say,
(see Wiki entry) The
definition for two continum signals f(t) and g(t)
is Velocity conventions
(RAD,OPT,REL): There are usually three types of velocity conventions used
in radio astronomy:
V(OPT) = c*z = c*(lambda-lambda0)/lambda0 = c*(f0-f)/f
First of all, a calibration scale temperature TC will be derived by alternatively TC = [T(vane) - T_A(sky)] / eta_l / eta_fss / exp(-tau0*A) Typical value of TC = 400 K for SSB and 800K for DSB at the ARO 12m telescope
(these are values used in practical observations). But it will vary with efficiency
factors (eta_l and eta_fss), temperature (T(vane)), atmospheric opacity (tau0) and airmass (A).
Then, a gain array will be computed for each spectral channel. Ci = (Rci-Zi) / (Sci-Rci) * TC. Ci is the effective system temperature for spectral channel i, Rci, Sci and Zi are receiver response
to the calibration reference (cold sky), calibration signal (vane) and no signal.
The average of Ci over all channels is the shown system temperature in the data header: Tsys = <Ci> Note that, if a two-channel receiver is in use, Tsys is an average of both receiver channels.
Finally, the calibrated antenna temperature T*_R is (T*_R)i = (Si-Ri)/(Ri-Zi) * Ci. Here Si and Ri are the receiver response at the on-source and off-source positions. (my comment: This formula is correct only when the effective system temperature Ci during the vane calibration
is equal to the that during the off-position observation of the program star. Otherwise,
extra uncertainty will be introduced.) Ci = TC / (Sci-Rci) where the terms are defined above. Then the antenna temperature is given by (T*R)i = (Si-Ri)*Ci |
|||||||
|
|